题目内容
已知函数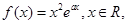 其中
其中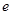 为自然对数的底数,
为自然对数的底数, 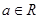 .
.
(1)设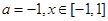 ,求函数
,求函数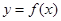 的最值;
的最值;
(2)若对于任意的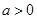 ,都有
,都有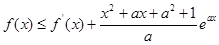 成立,求
成立,求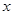 的取值范围.
的取值范围.
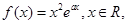 其中
其中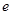 为自然对数的底数,
为自然对数的底数, 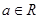 .
.(1)设
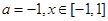 ,求函数
,求函数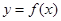 的最值;
的最值;(2)若对于任意的
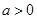 ,都有
,都有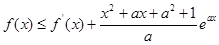 成立,求
成立,求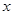 的取值范围.
的取值范围.(1)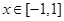 时,
时, ,
,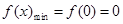 ;(2)
;(2)
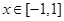 时,
时, ,
,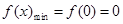 ;(2)
;(2)
试题分析:(1)将
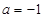 代入解析式,利用导函数求出驻点
代入解析式,利用导函数求出驻点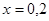 然后在
然后在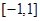 分析导函数的正负,从而得出函数的单调性求出最值
分析导函数的正负,从而得出函数的单调性求出最值 ,
,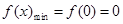 ;(2)将对于任意的
;(2)将对于任意的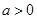 ,都有
,都有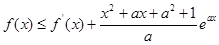 成立转化为对任意
成立转化为对任意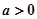 ,
,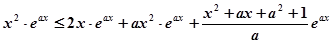 恒成立,然后利用参变分离求解即可.
恒成立,然后利用参变分离求解即可.试题解析:(1)当
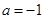 时,
时,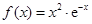 ,
,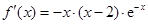 . 1分
. 1分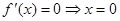 或
或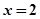 ,当
,当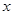 在
在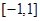 上变化时,
上变化时,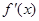 ,
,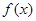 的变化情况如下表:
的变化情况如下表: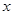 | 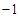 | 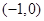 |  | 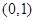 | 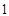 |
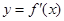 | | - |  | + | |
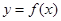 | 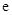 |  |  |  | 1/e |
∴
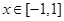 时,
时, ,
,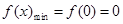 . 5分
. 5分(2)命题等价于对任意
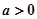 ,
,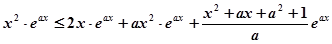 恒成立,
恒成立,即
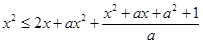 对任意
对任意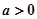 恒成立.
恒成立.则
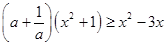 ,有
,有 ,
,又
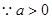
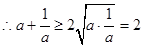 , 9′
, 9′只需
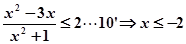 或
或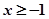 .
.综上:
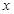 的取值范围为
的取值范围为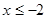 或
或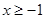 . 12′
. 12′
练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
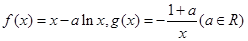 .
. 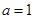 时,求曲线
时,求曲线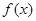 在
在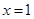 处的切线方程;
处的切线方程;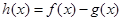 ,求函数
,求函数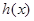 的单调区间;
的单调区间;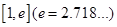 上存在一点
上存在一点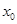 ,使得
,使得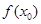 <
<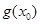 成立,求
成立,求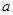 的取值范围.
的取值范围.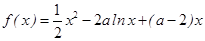
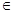 (0,+∞),且x1≠x2,都有
(0,+∞),且x1≠x2,都有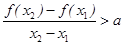 恒成立.若存在,求出a的取值范围;若不存在,说明理由.
恒成立.若存在,求出a的取值范围;若不存在,说明理由.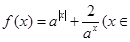 R,
R,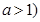 ,
,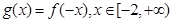 ,若
,若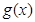 的最小值与
的最小值与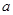 无关,求
无关,求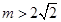 ,直接写出(不需给出演算步骤)关于
,直接写出(不需给出演算步骤)关于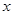 的方程
的方程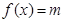 的解集
的解集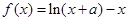 的最大值为0,其中
的最大值为0,其中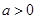 。
。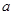 的值;
的值; 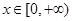 ,有
,有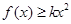 成立,求实数
成立,求实数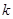 的最大值;
的最大值;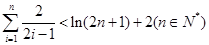
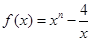 ,且
,且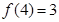 .
.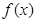 的奇偶性并说明理由;
的奇偶性并说明理由;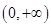 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;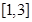 上,不等式
上,不等式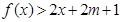 恒成立,试确定实数
恒成立,试确定实数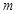 的取值范围.
的取值范围.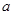 为常数,函数
为常数,函数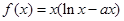 有两个极值点
有两个极值点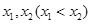 ,则( )
,则( )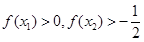
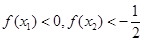
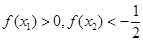
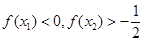
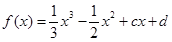 有极值,则
有极值,则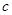 的取值范围为( )
的取值范围为( )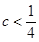
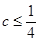
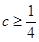
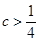
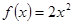 ,则
,则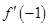 等于 .
等于 .