题目内容
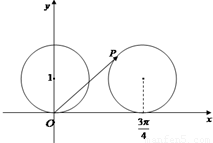 如图,在平面直角坐标系中,一单位圆的圆心的初始位置在(0,1),此时P点位置是原点,圆在x轴上沿正向滚动,当圆滚动到圆心位于(
如图,在平面直角坐标系中,一单位圆的圆心的初始位置在(0,1),此时P点位置是原点,圆在x轴上沿正向滚动,当圆滚动到圆心位于(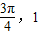 )时,
)时,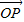 的坐标为 .
的坐标为 .
【答案】分析:设滚动后圆的圆心为O',切点为A,连接O'P.过O'作与x轴正方向平行的射线,交圆O'于B(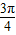 ,1),设∠BO'P=θ,则根据圆的参数方程,得P的坐标为(
,1),设∠BO'P=θ,则根据圆的参数方程,得P的坐标为(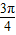 +cosθ,1+sinθ),再根据圆的圆心从(0,1)滚动到(
+cosθ,1+sinθ),再根据圆的圆心从(0,1)滚动到(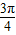 ,1),算出θ=
,1),算出θ=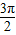 -
-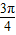 =
=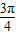 ,结合三角函数的诱导公式,化简可得P的坐标为(
,结合三角函数的诱导公式,化简可得P的坐标为(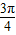 -sin
-sin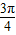 ,1-cos
,1-cos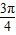 ),即为向量
),即为向量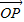 的坐标.
的坐标.
解答: 解:设滚动后的圆的圆心为O',切点为A(
解:设滚动后的圆的圆心为O',切点为A(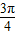 ,0),连接O'P,
,0),连接O'P,
过O'作与x轴正方向平行的射线,交圆O'于B(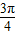 +1,1),
+1,1),
设∠BO'P=θ
∵⊙O'的方程为(x-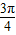 )2+(y-1)2=1,
)2+(y-1)2=1,
∴根据圆的参数方程,得P的坐标为(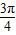 +cosθ,1+sinθ),
+cosθ,1+sinθ),
∵单位圆的圆心的初始位置在(0,1),圆滚动到圆心位于(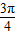 ,1)
,1)
∴∠AO'P=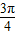 ,可得θ=
,可得θ=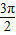 -
-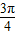 =
=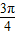
可得cosθ=-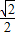 ,sinθ=
,sinθ=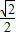
代入上面所得的式子,得到P的坐标为(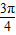 -
-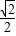 ,1+
,1+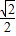 ),
),
∴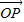 的坐标为(
的坐标为(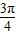 -
-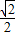 ,1+
,1+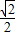 ),
),
故答案为:(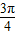 -
-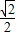 ,1+
,1+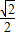 )
)
点评:本题根据半径为1的圆的滚动,求一个向量的坐标,着重考查了圆的参数方程和平面向量的坐标表示的应用等知识点,属于中档题.
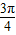 ,1),设∠BO'P=θ,则根据圆的参数方程,得P的坐标为(
,1),设∠BO'P=θ,则根据圆的参数方程,得P的坐标为(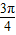 +cosθ,1+sinθ),再根据圆的圆心从(0,1)滚动到(
+cosθ,1+sinθ),再根据圆的圆心从(0,1)滚动到(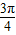 ,1),算出θ=
,1),算出θ=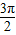 -
-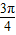 =
=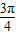 ,结合三角函数的诱导公式,化简可得P的坐标为(
,结合三角函数的诱导公式,化简可得P的坐标为(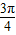 -sin
-sin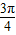 ,1-cos
,1-cos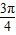 ),即为向量
),即为向量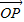 的坐标.
的坐标.解答:
 解:设滚动后的圆的圆心为O',切点为A(
解:设滚动后的圆的圆心为O',切点为A(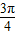 ,0),连接O'P,
,0),连接O'P,过O'作与x轴正方向平行的射线,交圆O'于B(
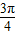 +1,1),
+1,1),设∠BO'P=θ
∵⊙O'的方程为(x-
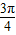 )2+(y-1)2=1,
)2+(y-1)2=1,∴根据圆的参数方程,得P的坐标为(
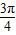 +cosθ,1+sinθ),
+cosθ,1+sinθ),∵单位圆的圆心的初始位置在(0,1),圆滚动到圆心位于(
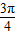 ,1)
,1)∴∠AO'P=
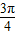 ,可得θ=
,可得θ=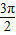 -
-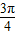 =
=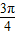
可得cosθ=-
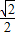 ,sinθ=
,sinθ=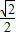
代入上面所得的式子,得到P的坐标为(
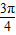 -
-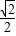 ,1+
,1+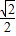 ),
),∴
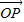 的坐标为(
的坐标为(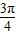 -
-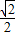 ,1+
,1+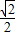 ),
),故答案为:(
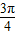 -
-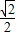 ,1+
,1+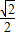 )
)点评:本题根据半径为1的圆的滚动,求一个向量的坐标,着重考查了圆的参数方程和平面向量的坐标表示的应用等知识点,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
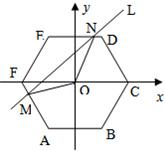 如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )
如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )| A、偶函数 | B、奇函数 | C、不是奇函数,也不是偶函数 | D、奇偶性与k有关 |
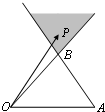 如图,在△OAB中,点P是线段OB及线段AB延长线所围成的阴影区域(含边界)的任意一点,且
如图,在△OAB中,点P是线段OB及线段AB延长线所围成的阴影区域(含边界)的任意一点,且 1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
 (2008•海珠区一模)如图,在直角坐标平面内,射线OT落在60°的终边上,任作一条射线OA,OA落在∠xOT内的概率是
(2008•海珠区一模)如图,在直角坐标平面内,射线OT落在60°的终边上,任作一条射线OA,OA落在∠xOT内的概率是