题目内容
设△ABC的内角A,B,C所对的边长分别为a,b,c,且acosB-bcosA=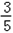 c.
c.
(I)求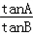 的值;
的值;
(II)求tan(A﹣B)的最大值.
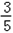 c.
c.(I)求
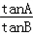 的值;
的值;(II)求tan(A﹣B)的最大值.
解:(Ⅰ)在△ABC中,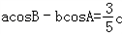 ,
,
由正弦定理得
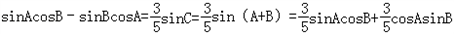
即sinAcosB=4cosAsinB,则
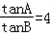 ;
;
(Ⅱ)由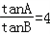 得
得
tanA=4tanB>0
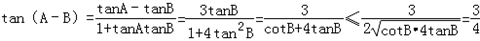
当且仅当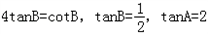 时,等号成立,
时,等号成立,
故当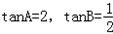 时,
时,
tan(A﹣B)的最大值为 .
.
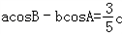 ,
,由正弦定理得
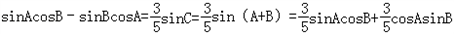
即sinAcosB=4cosAsinB,则
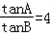 ;
;(Ⅱ)由
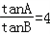 得
得tanA=4tanB>0
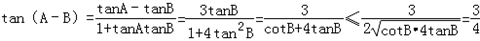
当且仅当
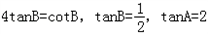 时,等号成立,
时,等号成立,故当
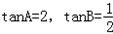 时,
时,tan(A﹣B)的最大值为
 .
.
练习册系列答案
相关题目