Question

如图，某地一天从6时至14时的温度变化曲线近似地满足函数y=Asin（ωx+φ）+b.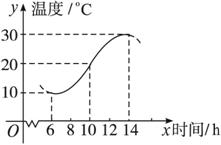

（1）求这段时间的最大温差；

（2）写出这段曲线的函数解析式.

Answer 1

思路分析:解决此问题的关键是根据图象确定A、ω、φ的值.

解：（1）由题图可知，这段时间的最大温差是30－10=20（℃）.

（2）图中从6时至14时的图象是函数y=Asin（ωx+φ）+b的半个周期的图象，

，解得ω＝.

由图知A=（30－10）=10，b=（30+10）=20.

这时y=10sin（+φ）+20.

将x=6，y=10代入上式，可得φ=.

综上，所求的解析式为y=10sin（）+20，x∈［6，14］.

方法归纳 在y=Asin（ωx+φ）中A表示振动量离开平衡位置的最大距离，可通过观察图象求值，若已知φ值及图象与y轴的交点，可列方程求A的值；ω与函数的周期有关，；φ可通过代点法求解，代点时最好代入最值点，当不存在最值点时，代点时应看点在图象上的位置是处在上升的位置还是处在下降的位置，从而来确定ωx+φ是在单调增区间内取值，还是在单调减区间内取值.一般地，当点处在上升的位置时，ωx+φ是在单调增区间内取值；当点处在下降的位置时，ωx+φ在单调减区间内取值.