题目内容
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于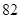 为正品,小于
为正品,小于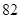 为次品.现随机抽取这两种元件各
为次品.现随机抽取这两种元件各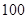 件进行检测,检测结果统计如下:
件进行检测,检测结果统计如下:
| 测试指标 | 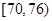 | 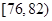 | 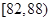 | 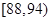 | 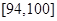 |
| 元件A | 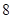 | 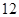 | 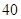 | 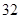 | 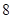 |
| 元件B | 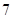 | 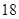 | 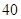 | 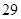 | 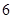 |
(Ⅱ)生产一件元件A,若是正品可盈利40元,若是次品则亏损5元;生产一件元件B,若是正品可盈利50元,若是次品则亏损10元.在(Ⅰ)的前提下,
(ⅰ)记
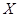 为生产1件元件A和1件元件B所得的总利润,求随机变量
为生产1件元件A和1件元件B所得的总利润,求随机变量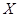 的分布列和数学期望;
的分布列和数学期望;(ⅱ)求生产5件元件B所获得的利润不少于140元的概率.
(Ⅰ)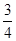 (Ⅱ)(ⅰ)66 (ⅱ)
(Ⅱ)(ⅰ)66 (ⅱ)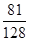
解析试题分析:(Ⅰ)解:元件A为正品的概率约为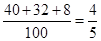 .
.
元件B为正品的概率约为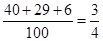 .
.
(Ⅱ)解:(ⅰ)随机变量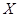 的所有取值为
的所有取值为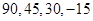 .
. 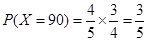 ;
;  ;
;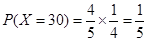 ;
; 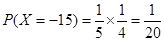 .
.
所以,随机变量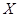 的分布列为:
的分布列为: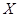
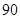
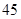
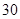
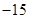
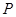
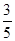
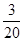
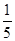
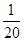
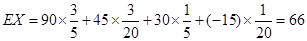 .
.
(ⅱ)设生产的5件元件B中正品有 件,则次品有
件,则次品有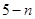 件.
件.
依题意,得 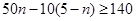 , 解得
, 解得 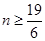 .
.
所以 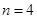 ,或
,或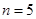 .
.
设“生产5件元件B所获得的利润不少于140元”为事件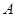 ,
,
则 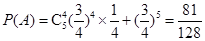 .
.
考点:离散型随机变量及其分布列;离散型随机变量的期望与方差.
点评:熟练掌握分类讨论的思想方法、古典概型的概率计算公式、相互独立事件的概率计算公式、数学期望的定义、二项分布列的计算公式是解题的关键.

练习册系列答案
相关题目
 ,得到黑球或黄球的概率是
,得到黑球或黄球的概率是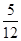 ,得到黄球或绿球的概率是
,得到黄球或绿球的概率是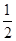 ,试求得到黑球、黄球、绿球的概率各是多少?
,试求得到黑球、黄球、绿球的概率各是多少?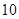 道题中,甲答对其中每道题的概率都是
道题中,甲答对其中每道题的概率都是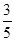 ,乙能答对其中的
,乙能答对其中的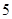 道题.规定每次考试都从备选的
道题.规定每次考试都从备选的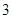 道题进行测试,答对一题加
道题进行测试,答对一题加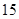 分才能入选.
分才能入选.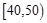 ,
, ,…,
,…, 后得到如下频率分布直方图.
后得到如下频率分布直方图.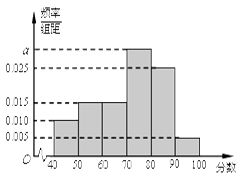
 的值
的值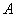 、
、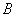 、
、 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是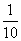 ,
, 、
、 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是 ,只要遇到拥堵上学和上班的都会迟到.
,只要遇到拥堵上学和上班的都会迟到.
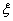 表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求
表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求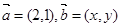
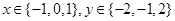 ,求向量
,求向量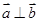 的概率;
的概率;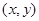 构成区域
构成区域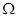 :
: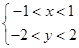 ,求二元数组
,求二元数组
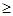 1的概率.
1的概率.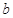 和
和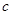 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量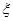 表示方程
表示方程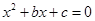 实根的个数(重根按一个计).
实根的个数(重根按一个计).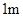 、
、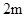 、
、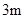 的钢管各
的钢管各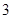 根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取
根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取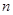 根(假设各钢管被抽取的可能性是均等的,
根(假设各钢管被抽取的可能性是均等的, ),再将抽取的钢管相接焊成笔直的一根.
),再将抽取的钢管相接焊成笔直的一根.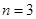 时,记事件
时,记事件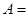 {抽取的
{抽取的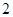 根长度相等},求
根长度相等},求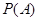 ;
;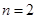 时,若用
时,若用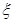 表示新焊成的钢管的长度(焊接误差不计),①求
表示新焊成的钢管的长度(焊接误差不计),①求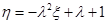 ,
,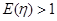 ,求实数
,求实数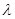 的取值范围.
的取值范围.