题目内容
已知向量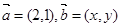
(Ⅰ)若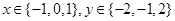 ,求向量
,求向量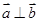 的概率;
的概率;
(Ⅱ)若用计算机产生的随机二元数组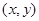 构成区域
构成区域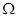 :
: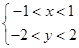 ,求二元数组
,求二元数组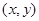 满足
满足
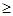 1的概率.
1的概率.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) 。
。
解析试题分析:(Ⅰ)从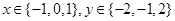 取两个数
取两个数 的基本事件有
的基本事件有
 ,共9种 2分
,共9种 2分
设“向量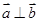 ”为事件
”为事件
若向量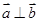 ,则
,则 3分
3分
∴事件 包含的基本事件有
包含的基本事件有 ,共2种 5分
,共2种 5分
∴所求事件的概率为 6分
6分
(Ⅱ)二元数组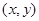 构成区域
构成区域

设“二元数组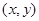 满足
满足
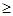 1”为事件
1”为事件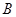
则事件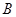

 9分
9分
∴所求事件的概率为 12分
12分
考点:本题主要考查古典概型、几何概型概率的计算。
点评:典型题,本题难度不大,较为典型,古典概型概率的计算,关键是计算事件数,可采用“树图法”“坐标法”,以保证不重不漏。几何概型概率的计算,关键是计算“几何度量”,往往与面积,体积,线段长度等有关。

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
山东省某示范性高中为了推进新课程改革,满足不同层次学生的需求,决定从高一年级开始,在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座,每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座.(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各学科讲座各天的满座概率如下表:
| | 信息技术 | 生物 | 化学 | 物理 | 数学 |
| 周一 | 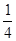 | 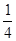 | 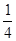 | 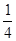 |  |
| 周三 |  |  |  |  | 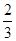 |
| 周五 |  |  |  |  | 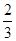 |
(Ⅱ)设周三各辅导讲座满座的科目数为
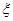 ,求随即变量
,求随即变量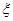 的分布列和数学期望.
的分布列和数学期望. 生产A,B两种元件,其质量按测试指标划分为:指标大于或等于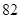 为正品,小于
为正品,小于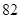 为次品.现随机抽取这两种元件各
为次品.现随机抽取这两种元件各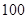 件进行检测,检测结果统计如下:
件进行检测,检测结果统计如下:
| 测试指标 | 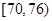 | 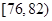 | 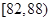 | 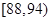 | 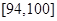 |
| 元件A | 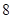 | 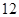 | 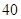 | 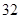 | 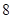 |
| 元件B | 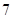 | 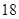 | 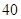 | 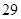 | 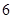 |
(Ⅱ)生产一件元件A,若是正品可盈利40元,若是次品则亏损5元;生产一件元件B,若是正品可盈利50元,若是次品则亏损10元.在(Ⅰ)的前提下,
(ⅰ)记
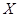 为生产1件元件A和1件元件B所得的总利润,求随机变量
为生产1件元件A和1件元件B所得的总利润,求随机变量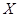 的分布列和数学期望;
的分布列和数学期望;(ⅱ)求生产5件元件B所获得的利润不少于140元的概率.
我区高三期末统一测试中某校的数学成绩分组统计如下表:
| 分组 | 频数 | 频率 |
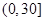 | 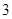 | 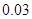 |
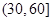 | 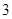 | 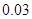 |
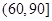 | 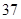 | 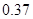 |
 | 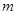 | 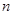 |
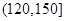 | 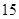 | 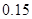 |
| 合计 | 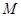 | 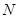 |
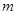 、
、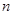 、
、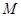 、
、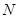 的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;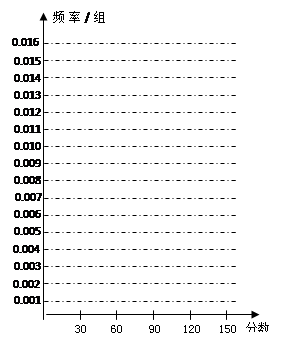
(2)若我区参加本次考试的学生有600人,试估计这次测试中我区成绩在
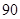 分以上的人数;
分以上的人数;(3)若该校教师拟从分数不超过60的学生中选取2人进行个案分析,求被选中2人分数不超过30分
的概率.
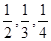 ,且每位同学能否通过考试时相互独立的。
,且每位同学能否通过考试时相互独立的。 ,求这三位同学中恰好有一位同学考上大学的概率。
,求这三位同学中恰好有一位同学考上大学的概率。 是从区间[0,3] 任 取 的一个数,
是从区间[0,3] 任 取 的一个数,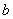 是从区间[0,2]任取的一个数,求上述方程有实根的概率.
是从区间[0,2]任取的一个数,求上述方程有实根的概率.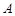 和
和 中装有若干个均匀的红球和白球,从
中装有若干个均匀的红球和白球,从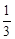 ,从
,从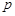 .
.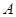 中有放回地摸球,每次摸出一个,共摸4次.
中有放回地摸球,每次摸出一个,共摸4次.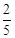 ,求
,求