题目内容
已知双曲线 的渐近线方程为
的渐近线方程为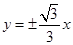 ,左焦点为F,过
,左焦点为F,过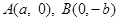 的直线为
的直线为 ,原点到直线
,原点到直线 的距离是
的距离是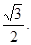
(1)求双曲线的方程;
(2)已知直线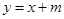 交双曲线于不同的两点C,D,问是否存在实数
交双曲线于不同的两点C,D,问是否存在实数 ,使得以CD为直径的圆经过双曲线的左焦点F。若存在,求出m的值;若不存在,请说明理由。
,使得以CD为直径的圆经过双曲线的左焦点F。若存在,求出m的值;若不存在,请说明理由。
(1)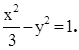 (2)
(2)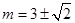 。
。
解析试题分析:(1)∵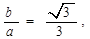 2分
2分
原点到直线AB: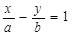 的距离,
的距离, 4分
4分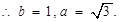 故所求双曲线方程为
故所求双曲线方程为 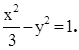 6分
6分
(2)把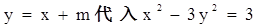 中消去y,整理得
中消去y,整理得 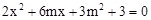 . 8分
. 8分
设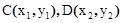 ,则
,则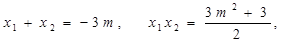
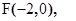
因为以CD为直径的圆经过双曲线的左焦点F,所以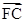
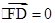 , 10分
, 10分
可得 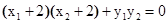 把
把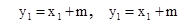 代入,
代入,
解得: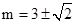 11分
11分
解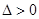 ,得
,得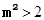 ,
,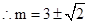 满足
满足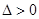 ,
,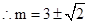 12分
12分
考点:双曲线的标准方程;双曲线的简单性质;直线与双曲线的综合应用。
点评:直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题等.突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法.

练习册系列答案
相关题目
 的极坐标方程为
的极坐标方程为 ,以极点为直角坐标系的原点,极轴为
,以极点为直角坐标系的原点,极轴为 轴正半轴,两坐标系长度单位一致,建立平面直角坐标系.过圆
轴正半轴,两坐标系长度单位一致,建立平面直角坐标系.过圆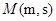 作平行于
作平行于 轴的直线
轴的直线 ,设
,设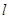 与
与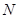 ,向量
,向量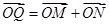 .
.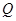 的轨迹方程;
的轨迹方程;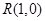 ,求
,求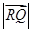 的最小值.
的最小值. 的长轴长为
的长轴长为 ,离心率为
,离心率为 ,
, 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点 ,且与直线
,且与直线 相切.
相切. 及动圆圆心轨迹
及动圆圆心轨迹 的方程;
的方程; 、
、 ,椭圆
,椭圆 、
、 ,满足
,满足 与
与 共线,
共线, 与
与 共线,且
共线,且 ,求四边形
,求四边形 面积的最小值.
面积的最小值. 分别是椭圆的
分别是椭圆的 左,右焦点。
左,右焦点。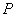 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且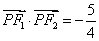 ,求点
,求点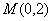 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点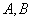 ,且
,且 为锐角(其中O为坐标原点),求直线
为锐角(其中O为坐标原点),求直线 的斜率
的斜率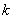 的取值范围。
的取值范围。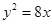 的焦点为右焦点,且经过点A(2,3).
的焦点为右焦点,且经过点A(2,3). 分别为椭圆的左右焦点,求
分别为椭圆的左右焦点,求 的角平分线所在直线的方程.
的角平分线所在直线的方程.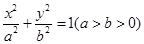 的离心率为
的离心率为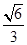 ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为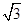 ,直线
,直线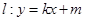 交椭圆于不同的两点
交椭圆于不同的两点 。
。 到直线
到直线 的距离为
的距离为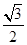 ,求
,求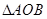 面积的最大值。
面积的最大值。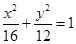 上找一点,使这一点到直线
上找一点,使这一点到直线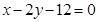 的距离为最小,并求最小值。
的距离为最小,并求最小值。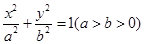 的左、右焦点分别为F1,F2,椭圆的离心率为
的左、右焦点分别为F1,F2,椭圆的离心率为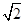 :2.(1)过点C(-1,0)且以向量
:2.(1)过点C(-1,0)且以向量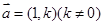 为方向向量的直线
为方向向量的直线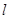 交椭圆于不同两点A、B,若
交椭圆于不同两点A、B,若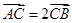 ,则当△OAB的面积最大时,求椭圆的方程。
,则当△OAB的面积最大时,求椭圆的方程。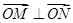 ,过原点O作直线MN的垂线OD,垂足为D,求点D的轨迹方程.
,过原点O作直线MN的垂线OD,垂足为D,求点D的轨迹方程.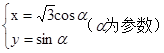 .
.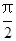 ),判断点P与直线L的位置关系;
),判断点P与直线L的位置关系;