题目内容
设 分别是椭圆的
分别是椭圆的 左,右焦点。
左,右焦点。
(Ⅰ)若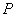 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且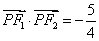 ,求点
,求点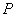 的坐标。
的坐标。
(Ⅱ)设过定点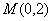 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点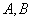 ,且
,且 为锐角(其中O为坐标原点),求直线
为锐角(其中O为坐标原点),求直线 的斜率
的斜率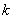 的取值范围。
的取值范围。
(Ⅰ) (Ⅱ)
(Ⅱ)
解析试题分析:(Ⅰ)易知 。
。
则 ,
,
联立
 ,解得
,解得
 ,
,
(Ⅱ)显然 可设
可设
联立

由
 得
得 ①
①
又 ,
, 又
又



 ②
②
综①②可知
考点:椭圆方程性质及直线与椭圆的位置关系
点评:直线与椭圆相交时常联立方程,利用韦达定理转化较简单,条件中将 转化为向量表示,进而与A,B坐标联系起来,即可利用韦达定理
转化为向量表示,进而与A,B坐标联系起来,即可利用韦达定理

练习册系列答案
相关题目
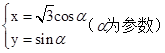 .
.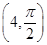 ,判断点P与直线l的位置关系;
,判断点P与直线l的位置关系;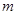 ,
,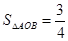 ;
; 的中心在原点,其上、下顶点分别为
的中心在原点,其上、下顶点分别为 ,点
,点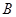 在直线
在直线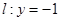 上,点
上,点 到椭圆的左焦点的距离为
到椭圆的左焦点的距离为 .
.
 是椭圆上异于
是椭圆上异于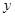 轴上的射影为
轴上的射影为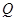 ,
,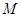 为
为 的中点,直线
的中点,直线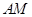 交直线
交直线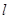 于点
于点 ,
, 为
为 的中点,试探究:
的中点,试探究: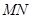 与圆
与圆 的位置关系,并证明你的结论.
的位置关系,并证明你的结论. 的上顶点为
的上顶点为 ,左焦点为
,左焦点为 ,直线
,直线 与圆
与圆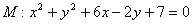 相切.过点
相切.过点 的直线与椭圆
的直线与椭圆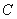 交于
交于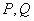 两点.
两点.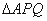 的面积达到最大时,求直线的方程.
的面积达到最大时,求直线的方程. ,点
,点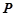 是点
是点 关于
关于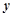 轴的对称点,过点
轴的对称点,过点 两点。
两点。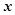 轴上是否存在不同于点
轴上是否存在不同于点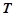 ,使得
,使得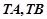 与
与 的面积为
的面积为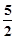 ,求向量
,求向量 的夹角;
的夹角; 的渐近线方程为
的渐近线方程为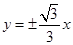 ,左焦点为F,过
,左焦点为F,过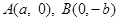 的直线为
的直线为 ,原点到直线
,原点到直线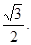
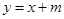 交双曲线于不同的两点C,D,问是否存在实数
交双曲线于不同的两点C,D,问是否存在实数 ,使得以CD为直径的圆经过双曲线的左焦点F。若存在,求出m的值;若不存在,请说明理由。
,使得以CD为直径的圆经过双曲线的左焦点F。若存在,求出m的值;若不存在,请说明理由。 的焦点为
的焦点为 ,过焦点
,过焦点 轴的动直线
轴的动直线 交抛物线于
交抛物线于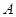 ,
, 两点,抛物线在
两点,抛物线在 .
.
 交该抛物线于
交该抛物线于 ,
,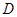 两点,求四边形
两点,求四边形 面积的最小值.
面积的最小值.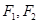 是椭圆的左、右焦点,O为坐标原点,点P
是椭圆的左、右焦点,O为坐标原点,点P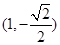 在椭圆上,线段
在椭圆上,线段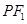 与y轴的交点M满足
与y轴的交点M满足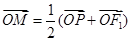
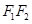 为直径的圆,直线
为直径的圆,直线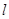 :
: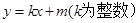 与圆相切,并与椭圆交于不同的两点
与圆相切,并与椭圆交于不同的两点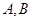 ,当
,当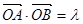 ,且满足
,且满足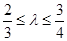 时,求直线
时,求直线