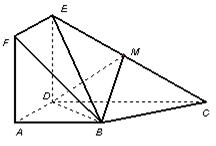
题目内容
如图,正方形![]() 与梯形
与梯形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() ,
,![]() ∥
∥![]() ,
,
![]() ,点
,点![]() 在线段
在线段![]() 上.
上.
(I)当点![]() 为
为![]() 中点时,求证:
中点时,求证:![]() ∥平面
∥平面![]() ;
;
(II)当平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
【考点分析】本小题主要考查空间线面位置关系的基本定理、多面体体积计算、(理)空间向量的应用,本小题主要考查空间想象能力、推理论证能力、运算求解能力.
解:(1)以直线![]() 、
、![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间
轴建立空间
直角坐标系,则![]() ,
,![]()
![]() ,
,![]() ,所以
,所以![]() .
.
 ∴
∴![]() ————————2分
————————2分
又,![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
∵![]() 即
即![]()
∴![]() ∥平面
∥平面![]() ——————4分
——————4分
(2)设![]() ,则
,则![]() ,
,
又![]()
设![]() ,则,
,则,![]() 即
即![]() .——6分
.——6分
设![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则
![]()
![]()
取![]() 得
得 ![]() 即
即 ![]()
又由题设,![]() 是平面
是平面![]() 的一个法向量,——————8分
的一个法向量,——————8分
∴  ————10分
————10分
即点![]() 为
为![]() 中点,此时,
中点,此时,![]() ,
,![]() 为三棱锥
为三棱锥![]() 的高,
的高,
∴ ![]()
![]() ————————————12分
————————————12分

练习册系列答案
相关题目
 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,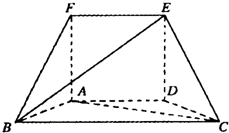 如图,正方形ADEF所在平面和等腰梯形所在平面ABCD垂直,已知BC=2AD=4,∠ABC=60°,BF⊥AC.
如图,正方形ADEF所在平面和等腰梯形所在平面ABCD垂直,已知BC=2AD=4,∠ABC=60°,BF⊥AC. 与梯形
与梯形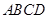 所在的平面互相垂直,
所在的平面互相垂直,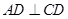 ,
,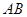 ∥
∥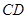 ,
,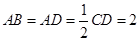 ,点
,点 在线段
在线段 上.
上.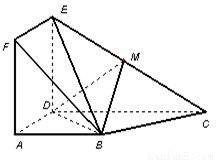
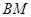 ∥平面
∥平面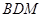 与平面
与平面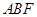 所成锐二面角的余弦值为
所成锐二面角的余弦值为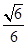 时,求三棱锥
时,求三棱锥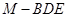 的体积.
的体积.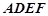 与梯形
与梯形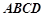 所在的平面互相垂直,
所在的平面互相垂直,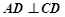 ,
,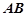 ∥
∥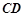 ,
,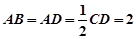 ,点
,点 在线段
在线段 上.
上.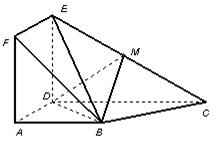
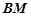 ∥平面
∥平面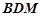 与平面
与平面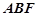 所成锐二面角的余弦值为
所成锐二面角的余弦值为 时,求三棱锥
时,求三棱锥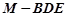 的体积.
的体积.