题目内容
已知偶函数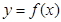 满足条件
满足条件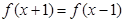 ,且当
,且当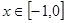 时,
时,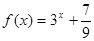 ,则
,则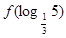 的值等于 。
的值等于 。
【答案】

【解析】
试题分析:因为偶函数 满足条件
满足条件 ,所以函数
,所以函数 的周期为2,所以
的周期为2,所以 。
。
考点:函数的奇偶性;函数的周期性,;对数函数的单调性;对数的运算。
点评:本题主要考查函数的奇偶性和周期性的灵活应用。
函数周期的判断:
① 函数y="f(x),x∈R," 若f(x+a)=f(x-a),则函数的周期为2|a|;
② 函数y="f(x),x∈R," 若f(x+a)=-f(x),则函数的周期为2|a|;
③ 函数y="f(x),x∈R," 若 ,则函数的周期为2|a|;
,则函数的周期为2|a|;
④ 若函数 的图象同时关于直线
的图象同时关于直线 与
与 对称,那么其周期为
对称,那么其周期为 。
。

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 满足:当
满足:当 时,
时, ,
,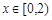 时,
时,
 时,
时, 的表达式;
的表达式; 满足什么条件时,函数
满足什么条件时,函数 有4个零点,
有4个零点, 满足条件:当
满足条件:当 时,恒有
时,恒有 ,且
,且 时,有
时,有 ,则
,则 的大小关系是 ( )
的大小关系是 ( )


