题目内容
已知偶函数 满足:当
满足:当 时,
时, ,
,
当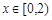 时,
时,
(1) 求当 时,
时, 的表达式;
的表达式;
(2) 试讨论:当实数 满足什么条件时,函数
满足什么条件时,函数 有4个零点,
有4个零点,
且这4个零点从小到大依次构成等差数列.
【答案】
(1) 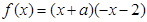 (2)见解析
(2)见解析
【解析】(1)因为f(x)为偶函数,只需用-x代替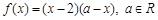 中的x即可得到当
中的x即可得到当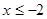 时,
时,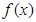 的表达式;
的表达式;
(2) 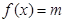 零点
零点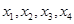 ,
,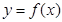 与
与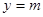 交点有4个且均匀分布.所以
交点有4个且均匀分布.所以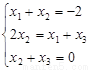 ,然后再分
,然后再分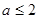 或
或 或
或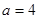 或
或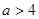 四种情况讨论求出m的值.解:(1)设
四种情况讨论求出m的值.解:(1)设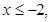 则
则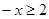 ,
,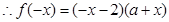
又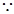
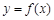 偶函数
偶函数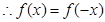
所以,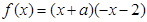 ………………………3分
………………………3分
(2)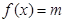 零点
零点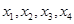 ,
,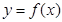 与
与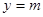 交点有4个且均匀分布
交点有4个且均匀分布
(Ⅰ)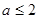 时,
时, 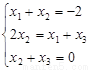 得
得 ,
,
所以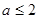 时,
时,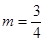 …………………………5分
…………………………5分
(Ⅱ) 且
且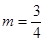 时 ,
时 ,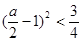 ,
, 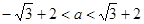
所以 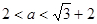 时,
时,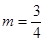 ……………………………7分
……………………………7分
(Ⅲ)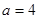 时m=1时 符合题意………………… ……8分
时m=1时 符合题意………………… ……8分
(IV)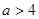 时,
时,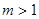 ,
,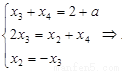
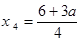 ,m
,m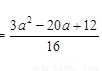
此时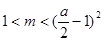 所以
所以 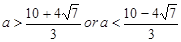 (舍)
(舍)
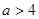 且
且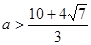 时,
时, 时存在 ………10分
时存在 ………10分
综上: ①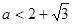 时,
时,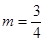
②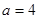 时,
时,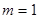
③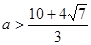 时,
时, 符合题意
………12分
符合题意
………12分

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 满足:当
满足:当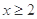 时,
时, ,当
,当 时,
时,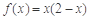 .
. 时,
时, 的表达式;
的表达式;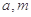 满足什么条件时,函数
满足什么条件时,函数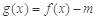 有4个零点,且这4个零点从小到大依次构成等差数列.
有4个零点,且这4个零点从小到大依次构成等差数列. 满足:当
满足:当 时,
时, ,当
,当 时,
时, .
. 表达式;
表达式; 与函数
与函数 的取值范围;
的取值范围;  满足什么条件时,直线
满足什么条件时,直线 的图像恰有
的图像恰有 个公共点
个公共点 ,且这
,且这 上.(不要求过程)
上.(不要求过程) 满足:当
满足:当 时,
时, ,当
,当 时,
时,
 时,
时, 的表达式;
的表达式; 与函数
与函数 的图象恰好有两个公共点,求实数
的图象恰好有两个公共点,求实数 的取值范围。
的取值范围。 满足什么条件时,函数
满足什么条件时,函数 有4个零点且这4个零点从小到大依次成等差数列。
有4个零点且这4个零点从小到大依次成等差数列。 满足:当
满足:当 时,
时,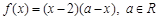 ,当
,当 时,
时,
 时,
时, 的表达式;
的表达式; 与函数
与函数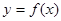 的图象恰好有两个公共点,求实数
的图象恰好有两个公共点,求实数 的取值范围。
的取值范围。 满足什么条件时,函数
满足什么条件时,函数 有4个零点且这4个零点从小到大依次成等差数列。
有4个零点且这4个零点从小到大依次成等差数列。