题目内容
(本小题满分14分)已知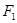 、
、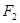 是椭圆
是椭圆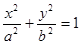 的两个焦点,O为坐标原点,点
的两个焦点,O为坐标原点,点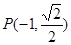 在椭圆上,线段
在椭圆上,线段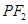 与
与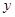 轴的交点
轴的交点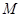 满足
满足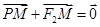 ;⊙O是以F1F2为直径的圆,一直线l:
;⊙O是以F1F2为直径的圆,一直线l: 与⊙O相切,并与椭圆交于不同的两点A、B.
与⊙O相切,并与椭圆交于不同的两点A、B.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)当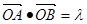 且满足
且满足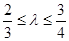 时,求△AOB面积S的取值范围.
时,求△AOB面积S的取值范围.
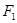 、
、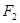 是椭圆
是椭圆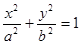 的两个焦点,O为坐标原点,点
的两个焦点,O为坐标原点,点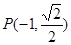 在椭圆上,线段
在椭圆上,线段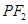 与
与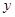 轴的交点
轴的交点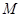 满足
满足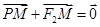 ;⊙O是以F1F2为直径的圆,一直线l:
;⊙O是以F1F2为直径的圆,一直线l: 与⊙O相切,并与椭圆交于不同的两点A、B.
与⊙O相切,并与椭圆交于不同的两点A、B.(Ⅰ)求椭圆的标准方程;
(Ⅱ)当
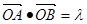 且满足
且满足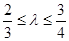 时,求△AOB面积S的取值范围.
时,求△AOB面积S的取值范围.(1)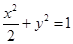 ;(2)
;(2)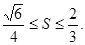 .
.
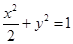 ;(2)
;(2)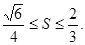 .
.第一问中利用 ,以及⊙O是以F1F2为直径的圆,可知
,以及⊙O是以F1F2为直径的圆,可知 ,得到a,bc的值,得到椭圆的方程
,得到a,bc的值,得到椭圆的方程
第二问中,利用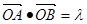 ,直线与圆相切,则可知圆心到直线的距离为1,然后得到
,直线与圆相切,则可知圆心到直线的距离为1,然后得到
 ,直线方程与椭圆联立方程组,结合韦达定理和向量的数量积公式得到结论。
,直线方程与椭圆联立方程组,结合韦达定理和向量的数量积公式得到结论。
解:(Ⅰ)
 点M是线段
点M是线段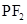 的中点
的中点  OM是
OM是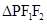 的中位线
的中位线
又

 解得
解得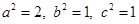
 椭圆的标准方程为
椭圆的标准方程为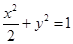 ………………………6分
………………………6分
(Ⅱ)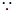 圆O与直线l相切
圆O与直线l相切 
 即:
即: ,由
,由
消去y: 设
设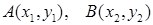
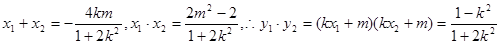 ,
,
 ,……………10分
,……………10分

设 , 则
, 则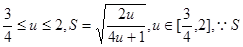 关于
关于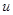 在
在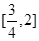 上单调
上单调
递增,且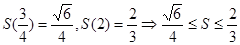
故△AOB面积S的取值范围是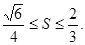 …………………………………………14分
…………………………………………14分
 ,以及⊙O是以F1F2为直径的圆,可知
,以及⊙O是以F1F2为直径的圆,可知 ,得到a,bc的值,得到椭圆的方程
,得到a,bc的值,得到椭圆的方程第二问中,利用
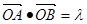 ,直线与圆相切,则可知圆心到直线的距离为1,然后得到
,直线与圆相切,则可知圆心到直线的距离为1,然后得到 ,直线方程与椭圆联立方程组,结合韦达定理和向量的数量积公式得到结论。
,直线方程与椭圆联立方程组,结合韦达定理和向量的数量积公式得到结论。解:(Ⅰ)

 点M是线段
点M是线段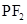 的中点
的中点  OM是
OM是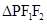 的中位线
的中位线又


 解得
解得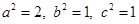
 椭圆的标准方程为
椭圆的标准方程为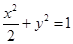 ………………………6分
………………………6分(Ⅱ)
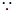 圆O与直线l相切
圆O与直线l相切 
 即:
即: ,由
,由
消去y:
 设
设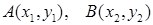
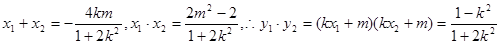 ,
, ,……………10分
,……………10分
设
 , 则
, 则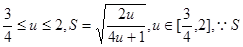 关于
关于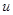 在
在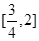 上单调
上单调递增,且
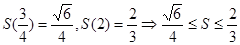
故△AOB面积S的取值范围是
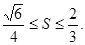 …………………………………………14分
…………………………………………14分
练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 的离心率
的离心率 ,过
,过 、
、 两点的直线到原点的距离是
两点的直线到原点的距离是 .
. 交椭圆于不同的两点
交椭圆于不同的两点 、
、 ,且
,且 为圆心的圆上,求
为圆心的圆上,求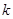 的值.
的值. 上的动点,F1,F2分别为其左、右焦点,O是坐标原点,则
上的动点,F1,F2分别为其左、右焦点,O是坐标原点,则 的取值范围是 .
的取值范围是 . +
+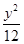 =1
=1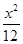 +
+ =1
=1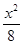 +
+ =1
=1 的一个焦点是
的一个焦点是 ,那么实数
,那么实数 的值为( )
的值为( )



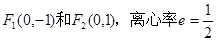
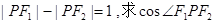 的值
的值 的左右焦点分别为F1,F2,离心率为e,若椭圆上存在点P,使得
的左右焦点分别为F1,F2,离心率为e,若椭圆上存在点P,使得 ,则该离心率e的取值范围是__________;
,则该离心率e的取值范围是__________; ,BM=
,BM= ,椭圆C以A,B为焦点且过点N.
,椭圆C以A,B为焦点且过点N.
 ,问是否存在不平行AB的直线L与椭圆C交于P,Q两点,且|PE|=|QE|,若存在,求出直线L与AB夹角的范围;若不存在,说明理由?
,问是否存在不平行AB的直线L与椭圆C交于P,Q两点,且|PE|=|QE|,若存在,求出直线L与AB夹角的范围;若不存在,说明理由? ,则椭圆的离心率为( )
,则椭圆的离心率为( )


