题目内容
计算:
(1)求复数z=
的共轭复数
(2)∫
|1-x|dx.
(1)求复数z=
| 1 |
| 1-i |
(2)∫
2 0 |
考点:复数代数形式的乘除运算,定积分
专题:数系的扩充和复数
分析:(1)利用复数的运算法则、共轭复数的定义即可得出;
(2)分区间积分即可去掉绝对值符号,再利用微积分基本定理即可得出.
(2)分区间积分即可去掉绝对值符号,再利用微积分基本定理即可得出.
解答:
解:(1)复数z=
=
=
+
i,其共轭复数
=
-
i.
(2)∫
|1-x|dx=
(1-x)d+
(x-1)dx=(x-
x2)
+(
x2-x)
=1.
| 1 |
| 1-i |
| 1+i |
| (1-i)(1+i) |
| 1 |
| 2 |
| 1 |
| 2 |
. |
| z |
| 1 |
| 2 |
| 1 |
| 2 |
(2)∫
2 0 |
| ∫ | 1 0 |
| ∫ | 2 1 |
| 1 |
| 2 |
| | | 1 0 |
| 1 |
| 2 |
| | | 2 1 |
点评:本题考查了复数的运算法则、分区间积分、微积分基本定理,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知点P是椭圆C上任一点,点P到直线l1:x=-2的距离为d1,到点F(-1,0)的距离为d2,且
已知点P是椭圆C上任一点,点P到直线l1:x=-2的距离为d1,到点F(-1,0)的距离为d2,且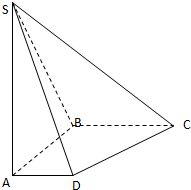 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=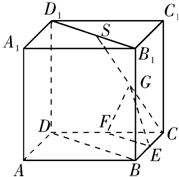 如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E、F、G分别是BC、CD和SC的中点.求证:
如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E、F、G分别是BC、CD和SC的中点.求证: