题目内容
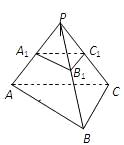 如图,已知三棱锥P-ABC的侧面PAC是底角为45°的等腰三角形,PA=PC,且该侧面垂直于底面,∠ACB=90°,AB=10,BC=6,B1C1=3.
如图,已知三棱锥P-ABC的侧面PAC是底角为45°的等腰三角形,PA=PC,且该侧面垂直于底面,∠ACB=90°,AB=10,BC=6,B1C1=3.
(1)求证:二面角A-PB-C是直二面角;
(2)求二面角P-AB-C的正切值;
(3)若该三棱锥被平行于底面的平面所截,得到一个几何体ABC-A1B1C1,求几何体ABC-A1B1C1的侧面积.
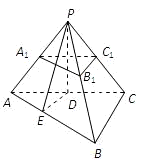 证明:(1)如图,在三棱锥P-ABC中,取AC的中点D.
证明:(1)如图,在三棱锥P-ABC中,取AC的中点D.由题设知△PAC是等腰直角三角形,且PA⊥PC.
∴PD⊥AC.
∵平面A1ACC1⊥平面ABC,∴PD⊥平面ABC,
∵AC⊥BC∴PA⊥BC,∴PA⊥平面PBC,
∵PA?平面PAB,∴平面PAB⊥平面PBC,
即二面角A-PB-C是直二面角.
解(2)作DE⊥AB,E为垂足,则PE⊥AB.
∴∠PED是二面角P-AB-C的平面角.
在Rt△ABC中,AB=10,BC=6,则AC=8,PD=4
由Rt△ADE~Rt△ABC,得
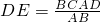 =
= =
= ,
,∴所求正切为
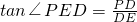 =
= .
.(3)∵
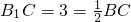 ∴A1,B1,C1分别是PA,PB,PC的中点.
∴A1,B1,C1分别是PA,PB,PC的中点.∴
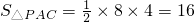 ,
,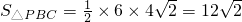 .
.∵
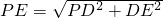 =
= =
= ,
,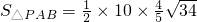 =
=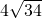 .
.∴S棱锥侧=
 ,
,∴几何体ABC-A1B1C1的侧面积
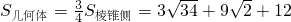 .
.分析:(1)欲证平面PAB⊥平面PBC,根据面面垂直的判定定理可知在平面PAB内一直线与平面PBC垂直,而根据题意可得PA⊥平面PBC,从而得到平面PAB⊥平面PBC,即二面角A-PB-C是直二面角;
(2)作DE⊥AB,E为垂足,则PE⊥AB,根据二面角平面角的定义可知∠PED是二面角P-AB-C的平面角,根据Rt△ADE~Rt△ABC可求出所求角的正切值;
(3)欲求几何体ABC-A1B1C1的侧面积,而SABC-A1B1C1=
 S三棱锥,可分别求出三棱锥的三个侧面面积即可.
S三棱锥,可分别求出三棱锥的三个侧面面积即可.点评:本题主要考查了二面角及其度量,以及棱台的侧面积和表面积,考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
 如图,已知三棱锥P-ABC中,PA⊥平面ABC,AN⊥BC于N,D是AB的中点,且PA=1,AN=BN=CN=
如图,已知三棱锥P-ABC中,PA⊥平面ABC,AN⊥BC于N,D是AB的中点,且PA=1,AN=BN=CN= 如图,已知三棱锥P-ABC中,PA⊥面ABC,其中正视图为Rt△PAC,AC=2
如图,已知三棱锥P-ABC中,PA⊥面ABC,其中正视图为Rt△PAC,AC=2 如图,已知三棱锥P-ABC的侧面PAB是等边三角形,D是AB的中点,PC=BC=AC=2,PB=2
如图,已知三棱锥P-ABC的侧面PAB是等边三角形,D是AB的中点,PC=BC=AC=2,PB=2 如图,已知三棱锥P-ABC,∠ACB=90°,CB=4,AB=20,D为AB中点,M为PB的中点,且△PDB是正三角形,PA⊥PC.
如图,已知三棱锥P-ABC,∠ACB=90°,CB=4,AB=20,D为AB中点,M为PB的中点,且△PDB是正三角形,PA⊥PC. (2009•河西区二模)如图,已知三棱锥P-ABC中,底面△ABC是边长为
(2009•河西区二模)如图,已知三棱锥P-ABC中,底面△ABC是边长为