题目内容
8．已知角A是△ABC的一个内角，且tanA=-$\frac{5}{4}$，求sinA，cosA的值．分析 根据同角的三角函数的关系进行求解即可．
解答 解：∵tanA=-$\frac{5}{4}$＜0，
∴A是钝角，则sinA＞0，cosA＜0，
∵sin2A=$\frac{sin^2A}{sin^2A+cos^2A}$=$\frac{ta{n}^{2}A}{1+ta{n}^{2}A}$=$\frac{\frac{25}{16}}{1+\frac{25}{16}}$=$\frac{25}{41}$．
∴sinA=$\sqrt{\frac{25}{41}}$=$\frac{5\sqrt{41}}{41}$，
cosA=-$\sqrt{1-si{n}^{2}A}$=-$\sqrt{1-\frac{25}{41}}$=-$\sqrt{\frac{16}{41}}$=-$\frac{4\sqrt{41}}{41}$．
点评 本题主要考查同角的三角关系的应用，考查学生的运算能力．
练习册系列答案
相关题目
18．函数$f（x）=\sqrt{{x^2}-2x-8}$的定义域为A，函数$g（x）=\frac{1}{{\sqrt{1-|{x-a}|}}}$的定义域为B，则使A∩B=∅的实数a的取值范围是（ ）
| A． | {a|-1＜a＜3} | B． | {a|-2＜a＜4} | C． | {a|-2≤a≤4} | D． | {a|-1≤a≤3} |
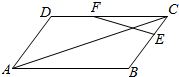如图，在?ABCD中，$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，$\overrightarrow{CE}$=$\frac{1}{3}$$\overrightarrow{CB}$，$\overrightarrow{CF}$=$\frac{2}{3}$$\overrightarrow{CD}$．
13．点P（x，y）满足平面区域：$\left\{\begin{array}{l}{cosθ≤x≤3cosθ}\\{sinθ≤y≤3sinθ}\end{array}\right.$（θ∈R），点M（x，y）满足：（x+5）2+（y+5）2=1，则|$\overrightarrow{PM}$|的最小值是（ ）
| A． | 5$\sqrt{2}$ | B． | 4$\sqrt{2}$-1 | C． | 6$\sqrt{2}$-1 | D． | $\sqrt{61}$-1 |
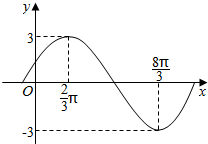已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象如图所示，f（x）=3sin（$\frac{1}{2}$x+$\frac{π}{6}$）．