题目内容
如图是某几何体的直观图与三视图的侧视图、俯视图.在直观图中,2BN=AE,M是ND的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.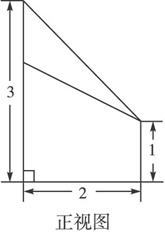
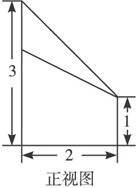
(1)画出该几何体的正视图,并标上数据;
(2)求证:EM∥平面ABC;
(3)试问在边BC上是否存在点G,使GN⊥平面NED.若存在,确定点G的位置;若不存在,请说明理由.
(1)解:正视图如图所示.(注:不标中间实线扣1分)
(2)证明:俯视图和侧视图,得∠CAB=90°,

DC=3,CA=AB=2,EA=2,BN=1,EA⊥平面ABC,
EA∥DC∥NB.取BC的中点F,连结FM、EM,
则FM∥DC∥EA,且FM=![]() (BN+DC)=2.
(BN+DC)=2.
∴FM![]() EA.∴四边形EAFM是平行四边形.
EA.∴四边形EAFM是平行四边形.
∴AF∥EM.又AF![]() 平面ABC,
平面ABC,
∴EM∥平面ABC.
(3)解:以A为原点,CA为x轴,AB为y轴,AE为z轴,建立如图所示的空间直角坐标系,
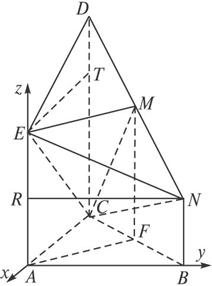
则有A(0,0,0),E(0,0,2),B(0,2,0),D(-2,0,3),N(0,2,1),C(-2,0,0).
设![]() =(-2,-2,2),
=(-2,-2,2),![]() =(0,-2,1),
=(0,-2,1),![]() =(2,2,0),
=(2,2,0),![]() =(2,2,1).
=(2,2,1).
假设在BC边上存在点G满足题意,
设![]() =λ
=λ![]() =(2λ,2λ,0),λ∈[0,1],
=(2λ,2λ,0),λ∈[0,1],
则![]() =
=![]() =(2,2,1)-(2λ,2λ,0)=(2-2λ,2-2λ,1).
=(2,2,1)-(2λ,2λ,0)=(2-2λ,2-2λ,1).
∵GN⊥平面NED,
∴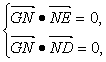 即
即![]()
解之,得λ=![]() ∈[0,1].
∈[0,1].
∴边BC上存在点G,满足CG=![]() CB时,GN⊥平面NED.
CB时,GN⊥平面NED.

练习册系列答案
相关题目
 如图是某几何体的三视图,它的正视图和侧视图均为矩形,俯视图为正三角形(长度单位:cm)
如图是某几何体的三视图,它的正视图和侧视图均为矩形,俯视图为正三角形(长度单位:cm)