Question

如图是某几何体的直观图与三视图的侧视图、俯视图.在直观图中，2BN=AE，M是ND的中点.侧视图是直角梯形，俯视图是等腰直角三角形，有关数据如图所示.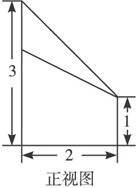

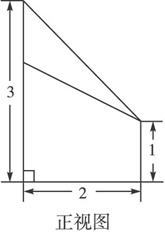
（1）画出该几何体的正视图，并标上数据；

（2）求证：EM∥平面ABC；

（3）求证：平面NDE⊥平面CEM.

Answer 1

解:（1）正视图如图所示.（注：不标中间实线扣1分）

（2）证明：俯视图和侧视图，得∠CAB=90°，DC=3，CA=AB=2，EA=2，BN=1，EA⊥ABC，

EA∥DC∥NB.取BC的中点F，连结FM、EM，则FM∥DC∥EA，且FM=（BN+DC）=2.∴FMEA，∴四边形EAFM是平行四边形.

∴AF∥EM.又AF平面ABC，∴EM平面ABC.

（3）证明:过N作NR⊥AE于R，则NR=2，RE=1，∴EN=.

过E作ET⊥CD于T，则ET=2，TD=1，∴ED=.∴ED=EN.

又M为DN的中点，∴EM⊥DN.连结CM、CN、CE.

∵BC=2，BN=1，BN⊥BC，∴CN=3.又CD=3，M为DN中点，

∴CM⊥DN，CM∩EM=M.∴DN⊥平面CEM，DN平面NDE.∴平面NDE⊥平面CEM.