题目内容
如图,在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ,
,
![]() ⊥底面
⊥底面![]() ,
,![]() ,
,![]() ,
,
![]() 是
是![]() 中点,点
中点,点![]() 在平面
在平面![]() 上的射影是△
上的射影是△![]()
的重心![]() .
.
(Ⅰ)求![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(II)求二面角![]() 的平面角的正弦值.
的平面角的正弦值.
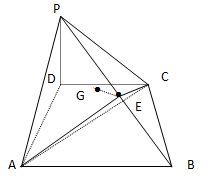
解:(Ⅰ)解:连结PG,则PG是PE在面ACP的射影,即∠EPG是PB与平面ACP所成的角. 设F为PA中点,连结EF、FD,



(II)
过点E作底面ABCD的垂线,垂足为H,则EH∥PD,且EH=1.
过点E作AC的垂线,垂足为I,连接HI,则∠HIE即为二面角![]() 的平面角。
的平面角。
由于CE∥DF,而DF⊥面PAB,所以CE⊥AE,CE⊥PB,可计算得CE=![]() ,AE=
,AE=![]() ,所以EI=
,所以EI=![]()
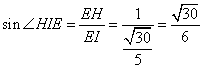
二面角![]() 的平面角的正弦值是
的平面角的正弦值是![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 中,底面
中,底面 是矩形.已知
是矩形.已知 .
.
 平面
平面 ;
; 与
与 所成的角的大小;
所成的角的大小; 的大小.
的大小. 中,底面
中,底面 是菱形,
是菱形, ,
, ,
, ,
, 平面
平面 是
是 的中点,
的中点, 是
是 的中点.
的中点.  ∥平面
∥平面 ;
; ;
; 所成的锐二面角的大小.
所成的锐二面角的大小.
 中,底面
中,底面 是矩形.已知
是矩形.已知 .
.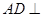 平面
平面 ;
; 与
与 所成的角的大小;
所成的角的大小; 的大小.
的大小.
 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 ,
, 为
为 中点,作
中点,作 交
交 于
于

 与平面
与平面 所成的锐二面角的正弦值。
所成的锐二面角的正弦值。 中,底面
中,底面 为平行四边形,
为平行四边形, 平面
平面

 在棱
在棱 上.
上.
 时,求证
时,求证 平面
平面
 的大小为
的大小为 时,求直线
时,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.