题目内容
7．某校医务室为了预防流感，准备从高一年级的10个班中抽取23名同学进行健康检查，要求每个班被抽到的同学不少于2人，那么不同的抽取方法共有（ ）| A． | 120种 | B． | 175种 | C． | 220种 | D． | 820种 |
分析 根据题意，先从每个班抽取2人，共抽取20人，将剩余的3个名额分配到10个班级，分3种情况讨论：①、3个名额分配到1个班级，②、3个名额分配到2个班级，③、3个名额分配到3个班级，分别求出每种下的抽取方法数目，由分类计数原理计算可得答案．
解答 解：根据题意，高一年级共10个班，每个班被抽到的同学不少于2人，
先从每个班抽取2人，共抽取20人，将剩余的3个名额分配到10个班级，分3种情况讨论：
①、3个名额分配到1个班级，在10个班级中抽取1个即可，有C101=10种抽取方法；
②、3个名额分配到2个班级，1个班级1个，1个班级2个，在10个班级中抽取2个，
再进行全排列即可，有C102×A22=90种抽取方法；
③、3个名额分配到3个班级，在10个班级中抽取3个即可，有C103=120种抽取方法；
则不同的抽取方法共有10+90+120=220种；
故选：C．
点评 本题考查排列、组合的应用，关键是转化问题，对多出的3个名额进行分类讨论，分配到10个班级．
练习册系列答案
相关题目
17．
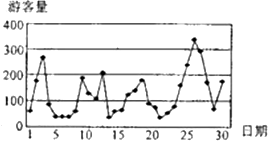已知云台山景区对拥挤等级与每日游客数量（单位：百人）的关系有如下规定：当n∈[0，100）时，拥挤等级为“优”；当n∈[100，200）时，拥挤等级为“良”；当n∈[200，300）时，拥挤等级为“拥挤”；当n≥300时，拥挤等级为“严重拥挤”．该景区对9月份的游客数量作出如图的统计数据．
（1）下面是根据统计数据得到的频率分布直方表，求出a，b，c的值，并估计该景区9月份游客人数的平均值（同一组中的数据用该组区间的中点值作代表）；
（2）某人选择在9月1日至9月5日这5天中任选2天到该景区游玩，求他这2天遇到的游客拥挤等级均为“优”的概率．
已知云台山景区对拥挤等级与每日游客数量（单位：百人）的关系有如下规定：当n∈[0，100）时，拥挤等级为“优”；当n∈[100，200）时，拥挤等级为“良”；当n∈[200，300）时，拥挤等级为“拥挤”；当n≥300时，拥挤等级为“严重拥挤”．该景区对9月份的游客数量作出如图的统计数据．（1）下面是根据统计数据得到的频率分布直方表，求出a，b，c的值，并估计该景区9月份游客人数的平均值（同一组中的数据用该组区间的中点值作代表）；
| 游客数量 （单位：百人） | [0，100） | [100，200） | [200，300） | [300，400） |
| 天数 | a | 10 | 4 | c |
| 频率 | b | $\frac{1}{3}$ | $\frac{2}{15}$ | $\frac{1}{30}$ |
15．已知复数z满足（$\sqrt{3}$+3i）z=3i，则|z|=（ ）
| A． | $\sqrt{2}$ | B． | 1 | C． | $\sqrt{3}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
2．下面中的两个变量，具有相关关系的是（ ）
| A． |  | B． |  | C． |  | D． |  |
19．为了调查某高中学生每天的睡眠时间，现随机对20名男生和20名女生进行问卷调查，结果如下：
（1）根据以上数据完成2×2列联表；
（2）是否有90%的把握认为“睡眠时间与性别有关”？
附临界参考表
附：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$．
| 睡眠时间（小时） | [4，5） | [5，6） | [6，7） | [7，8） | [8，9] |
| 女生人数 | 2 | 4 | 8 | 4 | 2 |
| 男生人数 | 1 | 5 | 6 | 5 | 3 |
（2）是否有90%的把握认为“睡眠时间与性别有关”？
| 睡眠时间少于7小时 | 睡眠时间不少于7小时 | 合计 | |
| 男生 | 12 | 8 | 20 |
| 女生 | 14 | 6 | 20 |
| 合计 | 26 | 14 | 40 |
| P（k2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
16．?x∈[-2，1]，使不等式ax3-x2+4x+3≥0成立，则实数a的取值范围是（ ）
| A． | [-5，-3] | B． | [-6，-$\frac{9}{8}$] | C． | [-6，-2] | D． | [-4，-3] |
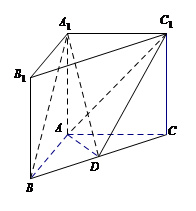如图，在直三棱柱A1B1C1-ABC中，AB=AC=AA1，$BC=\sqrt{2}AB$，点D是BC的中点．