题目内容
设函数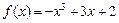 分别在
分别在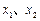 处取得极小值、极大值.
处取得极小值、极大值.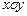 平面上点
平面上点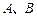 的坐标分别为
的坐标分别为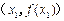 、
、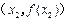 ,该平面上动点
,该平面上动点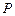 满足
满足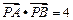 ,点
,点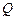 是点
是点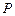 关于直线
关于直线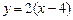 的对称点,.求
的对称点,.求
(Ⅰ)求点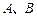 的坐标;
的坐标;
(Ⅱ)求动点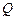 的轨迹方程.
的轨迹方程.
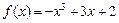 分别在
分别在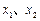 处取得极小值、极大值.
处取得极小值、极大值.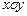 平面上点
平面上点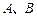 的坐标分别为
的坐标分别为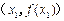 、
、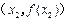 ,该平面上动点
,该平面上动点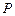 满足
满足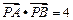 ,点
,点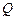 是点
是点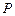 关于直线
关于直线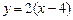 的对称点,.求
的对称点,.求(Ⅰ)求点
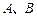 的坐标;
的坐标;(Ⅱ)求动点
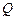 的轨迹方程.
的轨迹方程.解: (1)令 解得
解得
当 时,
时, , 当
, 当 时,
时, ,当
,当 时,
时,
所以,函数在 处取得极小值,在
处取得极小值,在 取得极大值,故
取得极大值,故 ,
,
所以, 点A、B的坐标为 .
.
(2) 设 ,
, ,
,
 ,所以
,所以 ,又PQ的中点在
,又PQ的中点在 上,
上,
所以
消去 得
得 .
.
另法:点P的轨迹方程为 其轨迹为以(0,2)为圆心,半径为3的圆;设点(0,2)关于y=2(x-4)的对称点为(a,b),则点Q的轨迹为以(a,b),为圆心,半径为3的圆,由
其轨迹为以(0,2)为圆心,半径为3的圆;设点(0,2)关于y=2(x-4)的对称点为(a,b),则点Q的轨迹为以(a,b),为圆心,半径为3的圆,由 ,
, 得a=8,b=-2
得a=8,b=-2
 解得
解得
当
 时,
时, , 当
, 当 时,
时, ,当
,当 时,
时,
所以,函数在
 处取得极小值,在
处取得极小值,在 取得极大值,故
取得极大值,故 ,
,
所以, 点A、B的坐标为
 .
.(2) 设
 ,
, ,
,
 ,所以
,所以 ,又PQ的中点在
,又PQ的中点在 上,
上,所以

消去
 得
得 .
.另法:点P的轨迹方程为
 其轨迹为以(0,2)为圆心,半径为3的圆;设点(0,2)关于y=2(x-4)的对称点为(a,b),则点Q的轨迹为以(a,b),为圆心,半径为3的圆,由
其轨迹为以(0,2)为圆心,半径为3的圆;设点(0,2)关于y=2(x-4)的对称点为(a,b),则点Q的轨迹为以(a,b),为圆心,半径为3的圆,由 ,
, 得a=8,b=-2
得a=8,b=-2略

练习册系列答案
相关题目
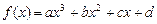 (a、b、c、d∈R)满足:对于任意的
(a、b、c、d∈R)满足:对于任意的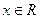 都有f(x)+f(-x)=0,且x=1时f(x)取极小值
都有f(x)+f(-x)=0,且x=1时f(x)取极小值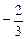 .
. 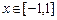 时,证明:函数图象上
时,证明:函数图象上 任意两点处的切线不可能互相垂直:
任意两点处的切线不可能互相垂直: .
. +
+ +2=0对定义域内的所有
+2=0对定义域内的所有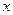 都成立;
都成立; +
+ ,
, -2];
-2];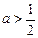 ,函数
,函数 =x2+|(x-
=x2+|(x-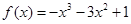 在
在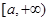 上的最大值为1,求a的取值范围( )
上的最大值为1,求a的取值范围( )



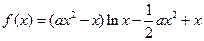 .
.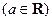 .
.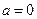 时,求曲线
时,求曲线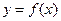 在
在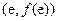 处的切线方程(
处的切线方程(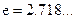 );
);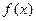 的单调区间.
的单调区间.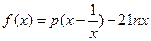 ,
,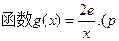 是实数,
是实数,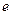 是自然对数的底数)
是自然对数的底数)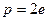 时,求
时,求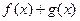 的单调区间;
的单调区间;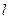 与函数
与函数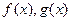 的图象都相切,且与函数
的图象都相切,且与函数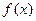 的图象相切于点(1,0),求P的值。
的图象相切于点(1,0),求P的值。 两地相距
两地相距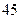 千米,
千米, 骑车人与客车分别从
骑车人与客车分别从 地的距离
地的距离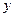 与时间
与时间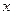 的函数关系.客车
的函数关系.客车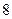 点从
点从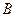 地出发,以
地出发,以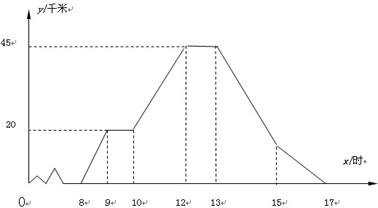
 图的基础上,直接回答:
图的基础上,直接回答: 骑车人共休息几次?骑车人总共骑行多少千米?骑车人与客车总共相遇几次?
骑车人共休息几次?骑车人总共骑行多少千米?骑车人与客车总共相遇几次? 出演算过程).
出演算过程).