题目内容
已知{an}是首项为a1,公比为q(q≠1)的等比数列,其前n项和为Sn,且有 ,设bn=2q+Sn
,设bn=2q+Sn
(1)求q的值;
(2)数列{bn}能否为等比数列?若能,请求出a1的值;若不能,请说明理由;
(3)在(2)的条件下,求数列{nbn}的前n项和Tn.
解(1)∵q≠1
∴ =
= =1+q5=
=1+q5=
∴
(2)由(1)知bn=2q+Sn=1+ =(2a1+1)-
=(2a1+1)-
①若数列{bn}能否为等比数列,则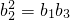 ,即
,即
∴ 或a1=0(舍去)
或a1=0(舍去)
∴
②∵bn≠0,且n≥2时,
∴ 时,数列{bn}为等比数列
时,数列{bn}为等比数列
(3)由(2)
∴
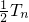 =
=
两式相减可得,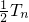 =
=
=
 =
=
∴Tn=2-
分析:(1)利用已知条件,利用等比数列的求和公式,列出关于等比数列的首项与公比的方程组,求公比
(2)由(1)知bn=2q+Sn=1+ =(2a1+1)-
=(2a1+1)- ,先假设数列{bn}能否为等比数列,则
,先假设数列{bn}能否为等比数列,则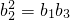 ,可求
,可求 ,
, ,代入检验即可判断
,代入检验即可判断
(3)由于bn是有一等差数列与等比数列的积构成的数列,利用错位相减的方法求出前n项和.
点评:求数列的前n项和,一般先求出通项,根据通项的特点选择合适的求和方法.
∴
 =
= =1+q5=
=1+q5=
∴

(2)由(1)知bn=2q+Sn=1+
 =(2a1+1)-
=(2a1+1)-
①若数列{bn}能否为等比数列,则
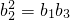 ,即
,即
∴
 或a1=0(舍去)
或a1=0(舍去)∴

②∵bn≠0,且n≥2时,

∴
 时,数列{bn}为等比数列
时,数列{bn}为等比数列(3)由(2)

∴

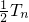 =
=
两式相减可得,
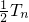 =
=
=

 =
=
∴Tn=2-

分析:(1)利用已知条件,利用等比数列的求和公式,列出关于等比数列的首项与公比的方程组,求公比
(2)由(1)知bn=2q+Sn=1+
 =(2a1+1)-
=(2a1+1)- ,先假设数列{bn}能否为等比数列,则
,先假设数列{bn}能否为等比数列,则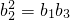 ,可求
,可求 ,
, ,代入检验即可判断
,代入检验即可判断(3)由于bn是有一等差数列与等比数列的积构成的数列,利用错位相减的方法求出前n项和.
点评:求数列的前n项和,一般先求出通项,根据通项的特点选择合适的求和方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知{an}是首项为1的等比数列,Sn是{an}的前n项和,且9S3=S6,则数列{
}的前5项和为( )
| 1 |
| an |
A、
| ||
B、
| ||
C、
| ||
D、
|