题目内容
已知函数f(x)＝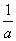
－
(a＞0, x＞0)，
(1)求证：f(x)在(0，＋∞)上是单调递增函数；
(2)若f(x)在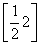
上的值域是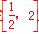
，求a的值．
(1)证明：设x2＞x1＞0，则x2－x1＞0，x1x2＞0，
－f(x1)＝
＝
－
＝
＞0，
∴f(x2)＞f(x1)，∴f(x)在(0，＋∞)上是单调递增函数．
(2)解析：∵f(x)在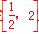上的值域是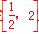，又f(x)在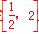上单调递增，
∴f
＝
，f(2)＝2.∴易得a＝
.
练习册系列答案
阅读快车系列答案
相关题目
C，AB的中点，点F为线段CD上的一点，将△ADE沿DE折起到△A1DE的位置，使A1F⊥CD，如图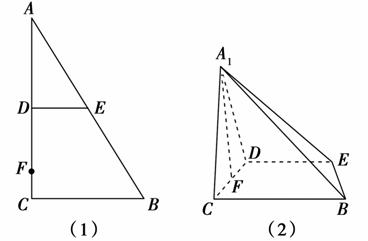(2)．
.
＝log2
的值域为( )
0
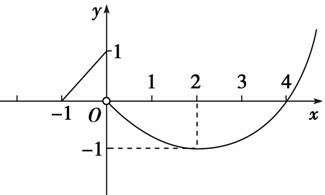
f(x)，g(x)分别是定义在R上的奇函数和偶函数，当x<0时，f′(x)g(x)＋f(x)g′(x)>0，且g(－3)＝0，则不等式f(x)g(x)<0的解集是________________．