题目内容
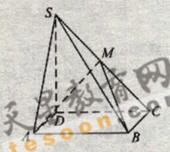
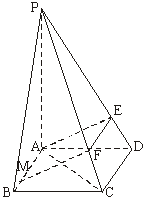
(19)如图，四棱锥P—ABCD的底面是正方形,PA⊥底面ABCD，AE⊥PD，EF∥CD，AM=EF.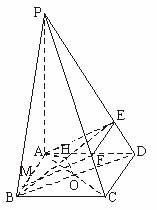
(Ⅰ)证明:MF是异面直线AB与PC的公垂线；
(Ⅱ)若PA=3AB，求直线AC与平面EAM所成角的正弦值.
(19)(Ⅰ)证明:因PA⊥底面，有PA⊥AB
又知AB⊥AD,故AB⊥面PAD，推得BA⊥AE.
又AM∥CD∥EF，且AM=EF，
证得AEFM是矩形，故AM⊥MF.
又因AE⊥PD，AE⊥CD，故AE⊥面PCD
因此MF是AB与PC的公垂线.
(Ⅱ)解：连结BD交AC于O，连结BE，过O作BE的垂线OH，
垂足H在BE上.
易知PD⊥面MAE，故DE⊥BE.
又OH⊥BE，故OH∥DE，
因此OH⊥面MAE.
连结AH，则∠HAO是所要求的直线AC与面MAE所成的角.
设AB=a,则PA=3a,AO=
AC=
a.
因Rt△ADE∽Rt△PDA,故
ED=
=
=
.
OH=
ED=
.
从而在Rt△AHO中,
sinHAO=
=
×
=
=
.
练习册系列答案
相关题目
中，底面
为矩形，
底面
，
，点
在侧棱
上，
。 
证明：
求二面角
的大小。 
