题目内容
(满分12分)
如图,四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是矩形.
(1)若PD=AD,E为PA的中点,求证:平面CDE⊥平面PAB;
(2)F是棱PC上的一点,CF=CP,问线段AC上是否存在一点M,使得PA∥平面DFM.若存在,指出点M在AC边上的位置,并加以证明;若不存在,说明理由.19. (满分12分)

【答案】
(1) ∵PD⊥底面ABCD, ∴PD⊥CD
又∵底面ABCD是矩形.∴CD⊥AD ∴CD⊥平面PAD
又PA 平面PAD ∴CD⊥PA
平面PAD ∴CD⊥PA
∵PD=AD,E为PA的中点 ∴DE⊥PA
CD∩DE=D ∴PA⊥平面CDE,
又PA 平面PAB ∴平面CDE⊥平面PAB.
平面PAB ∴平面CDE⊥平面PAB.
(2)在线段AC上存在点M,使得PA∥平面DFM,此时点M为靠近C点的一个四等分点,
证明如下:
连接AC.BD.设AC∩BD=O, PC的中点为G,连OG,则PA∥OG,
在ΔPAC中,∵CF=CP ∴F为CG的中点。
取OC的中点M,即CM=CA, 则MF∥OG, ∴MF∥PA
又PA 平面DFM, MF
平面DFM, MF 平面DFM ∴PA∥平面DFM .
平面DFM ∴PA∥平面DFM .
【解析】略

练习册系列答案
相关题目
 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, 底面
底面 ;
; 求二面角
求二面角 的余弦值.
的余弦值.
 平面BDE。
平面BDE。
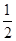 BD
BD

 的底面
的底面 为一直角梯形,其中
为一直角梯形,其中 ,
, 底面
底面 是
是 的中点.
的中点.
 //平面
//平面 ;
; 平面
平面 ,求异面直线
,求异面直线 与
与 所成角的余弦值;
所成角的余弦值;