Question

18．若方程（$\frac{1}{2}$）^x-2x+3=0的解为x=a，则（a-1）${\;}^{\frac{1}{2}}$与（a-1）${\;}^{\frac{1}{3}}$的大小关系是（a-1）${\;}^{\frac{1}{2}}$＜（a-1）${\;}^{\frac{1}{3}}$．

Answer 1

分析 求出a的范围，然后推出a-1的范围，即可利用指数函数的单调性判断（a-1）${\;}^{\frac{1}{2}}$与（a-1）${\;}^{\frac{1}{3}}$的大小．

解答 解：方程（$\frac{1}{2}$）^x-2x+3=0的解为x=a，
可得y=（$\frac{1}{2}$）^x与函数y=2x-3的图象如图：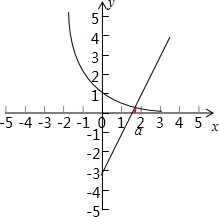

可得a∈$（\frac{3}{2}，2）$，a-1∈$（\frac{1}{2}，1）$．
y=（a-1）^x，是减函数，
所以（a-1）${\;}^{\frac{1}{2}}$＜（a-1）${\;}^{\frac{1}{3}}$．
故答案为：（a-1）${\;}^{\frac{1}{2}}$＜（a-1）${\;}^{\frac{1}{3}}$．

点评 本题考查函数的零点与方程根的关系，函数的图象的应用，考查计算能力．