题目内容
如图所示的空间直角坐标系A-xyz中,正三角形△ABC中AB=2,AA1∥BB1∥CC1,AA1=BB1=CC1=2,D,E分别为A1C,BB1的中点.
(Ⅰ)求证:DE∥平面ABC;
(Ⅱ)求异面直线BD与CE所成角的大小.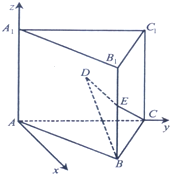
(Ⅰ)求证:DE∥平面ABC;
(Ⅱ)求异面直线BD与CE所成角的大小.

依题意,A(0,0,0),B(
,1,0),C(0,2,0),D(0,1,1),E(
,1,1)
(1)取AC的中点F(0,1,0),则
=(-
,0,0),
=(-
,0,0)
∴
=
∴DE∥BF
又BF?平面ABC,DE?平面ABC
∴DE∥平面ABC
(2)∵
=(-
,0,1),
=(
,-1,1)
∴cos<
,
>=
=
=-
∴异面直线BD与CE所成角的余弦值为
∴异面直线BD与CE所成角的大小为arccos
| 3 |
| 3 |
(1)取AC的中点F(0,1,0),则
| BF |
| 3 |
| ED |
| 3 |
∴
| BF |
| ED |
∴DE∥BF
又BF?平面ABC,DE?平面ABC
∴DE∥平面ABC
(2)∵
| BD |
| 3 |
| CE |
| 3 |
∴cos<
| BD |
| CE |
| ||||
|
|
| -3+0+1 | ||||
|
| ||
| 5 |
∴异面直线BD与CE所成角的余弦值为
| ||
| 5 |
∴异面直线BD与CE所成角的大小为arccos
| ||
| 5 |

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 三棱柱ABC-A1B1C1在如图所示的空间直角坐标系中,已知AB=2,AC=4,AA1=3.D是BC的中点.
三棱柱ABC-A1B1C1在如图所示的空间直角坐标系中,已知AB=2,AC=4,AA1=3.D是BC的中点. 在如图所示的空间直角坐标系中,AB=AD=2,AC=4,E,F分别是AD,BD的中点.
在如图所示的空间直角坐标系中,AB=AD=2,AC=4,E,F分别是AD,BD的中点. 已知ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=1,BC=2,E为PC的中点,PA⊥平面ABCD,建立如图所示的空间直角坐标系.
已知ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=1,BC=2,E为PC的中点,PA⊥平面ABCD,建立如图所示的空间直角坐标系. 如图所示的空间直角坐标系A-xyz中,正三角形△ABC中AB=2,AA1∥BB1∥CC1,AA1=BB1=CC1=2,D,E分别为A1C,BB1的中点.
如图所示的空间直角坐标系A-xyz中,正三角形△ABC中AB=2,AA1∥BB1∥CC1,AA1=BB1=CC1=2,D,E分别为A1C,BB1的中点. 在如图所示的空间直角坐标系O-xyz中,原点O是BC的中点,A点坐标为
在如图所示的空间直角坐标系O-xyz中,原点O是BC的中点,A点坐标为