题目内容
已知 p:f(x)=
,且|f(a)|<2;q:集合A={x|x2+(a+2)x+1=0,x∈R},B={x|x>0}且A∩B=∅.
若p∨q为真命题,p∧q为假命题,求实数a的取值范围.
| 1-x | 3 |
若p∨q为真命题,p∧q为假命题,求实数a的取值范围.
分析:结合f(x)=
,解绝对值不等式|f(a)|<2,我们可以求出p为真时参数a的取值范围;根据集合交集的定义及一元二次方程根的分布与系数的关系,可以判断q为真时参数a的取值范围;进而根据p∨q为真命题,p∧q为假命题,即p,q一真一假,分类讨论后,综合讨论结果,即可得到答案.
| 1-x |
| 3 |
解答:解:对p:所以|f (a)|=|
|<2.
若命题p为真,则有-5<a<7;
对q:∵B={x|x>0}且 A∩B=∅
∴若命题q为真,则方程g(x)=x2+(a+2)x+1=0无解或只有非正根.
∴△=(a+2)2-4<0或
,∴a>-4.
∵p,q中有且只有一个为真命题
∴(1)p 真,q假:则有
,即有-5<a≤-4;
(2)p 假,q 真:则有
,即有a≥7;
∴-5<a≤-4或a≥7.
| 1-a |
| 3 |
若命题p为真,则有-5<a<7;
对q:∵B={x|x>0}且 A∩B=∅
∴若命题q为真,则方程g(x)=x2+(a+2)x+1=0无解或只有非正根.
∴△=(a+2)2-4<0或
|
∵p,q中有且只有一个为真命题
∴(1)p 真,q假:则有
|
(2)p 假,q 真:则有
|
∴-5<a≤-4或a≥7.
点评:本题考查的知识点是命题的真假判断与应用,一元二次方程根的分面与系数的关系,由于两个命题为真时,求参数a的取值范围,都要用到转化思想,故本题难度稍大.

练习册系列答案
相关题目
 ,且|f(a)|<2;q:集合A={x|x2+(a+2)x+1=0,x∈R},B={x|x>0}且A∩B=∅.
,且|f(a)|<2;q:集合A={x|x2+(a+2)x+1=0,x∈R},B={x|x>0}且A∩B=∅.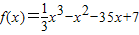 的导函数,且f'(a)<0;q:集合A={x|x2+(a+2)x+1=0,x∈R},B={ x|x>0},且A∩B=∅.求实数a的取值范围,使“p或q”为真命题,“p且q”为假命题.
的导函数,且f'(a)<0;q:集合A={x|x2+(a+2)x+1=0,x∈R},B={ x|x>0},且A∩B=∅.求实数a的取值范围,使“p或q”为真命题,“p且q”为假命题.