Question

已知p：f'（x）是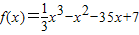的导函数，且f'（a）＜0；q：集合A={x|x²+（a+2）x+1=0，x∈R}，B={ x|x＞0}，且A∩B=∅．求实数a的取值范围，使“p或q”为真命题，“p且q”为假命题．

Answer 1

【答案】分析：先分别求命题p，q为真时，a的范围，p或q”为真命题，“p且q，则p，q一真一假，分p真q假和p假q真两种情况求出a的范围，而“p或q”为真命题，“p且q”为假命题，即“p，q一真一假”为假命题，所以，“p，q一真一假”的否命题为真，再求出刚才所求a的范围的补集即可．
解答：解：先考虑p：∵，
∴f'（x）=x²-2x-35，可得f'（a）=a²-2a-35＜0，解得：-5＜a＜7．
再考虑q：①当△＜0时，A=Φ，A∩B=Φ，
此时由（a+2）²-4＜0得-4＜a＜0； ②当△≥0时，
由A∩B=Φ可得：，解得a≥0．由①②可知a＞-4．（9分）
要使p真q假，则；要使p假q真，则，
综上所述，当a的范围是（-5，-4]∪[7，+∞）时，p、q中有且只有一个为真命题．（12分）
点评：本题考查了复合命题的真假判断，题目具有一定迷惑性，做题时须认真读题，找到正确方法．