题目内容
已知Sn是数列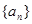 的前n项和,且
的前n项和,且
(Ⅰ)求数列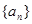 的通项公式;
的通项公式;
(Ⅱ)设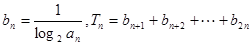 ,是否存在最大的正整数k,使得对于任意的正整数n,有
,是否存在最大的正整数k,使得对于任意的正整数n,有 恒成立?若存在,求出k的值;若不存在,说明理由.
恒成立?若存在,求出k的值;若不存在,说明理由.
【答案】
(1) (
(  );)(2)存在最大正整数 k=5使 ,
);)(2)存在最大正整数 k=5使 ,  恒成立
恒成立
【解析】:(Ⅰ)当 时,由已知
时,由已知 ………………①
………………①
得  …………②
…………②
②-①,得 
∴
∴
∴
所以数列  是一个以2为首项,2为公比的等比数列
是一个以2为首项,2为公比的等比数列
∴ (
(  )
)
(Ⅱ)
∴

∴

∵n是正整数, ∴
∴数列{Tn}是一个单调递增数列,又
∴ ,
,
要使  恒成立,则
恒成立,则
又k是正整数,故存在最大正整数 k=5使
,  恒成立
恒成立

练习册系列答案
相关题目
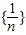 的前n项和;
的前n项和;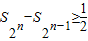 ,并指出等号成立条件;
,并指出等号成立条件; }的前n项和,则
}的前n项和,则 等于( )
等于( )


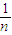 }的前n项和,
}的前n项和,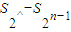 ≥
≥ ,并指出等号成立条件;
,并指出等号成立条件;