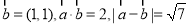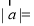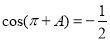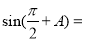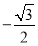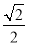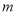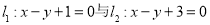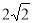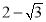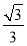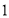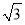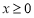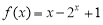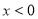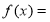题目内容
如图,在长方体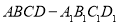 中,
中,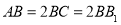 , 沿平面
, 沿平面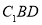 把这个长方体截成两个几何体: 几何体(1);几何体(2)
把这个长方体截成两个几何体: 几何体(1);几何体(2)
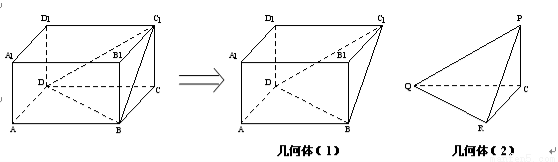
(I)设几何体(1)、几何体(2)的体积分为是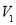 、
、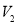 ,求
,求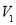 与
与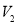 的比值
的比值
(II)在几何体(2)中,求二面角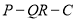 的正切值
的正切值
(I)5;(II) 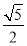
【解析】
试题分析:(I)先设出边长求长方体的体积,再求几何体(2)的体积 ,用长方体的体积减去
,用长方体的体积减去 即为几何体(1)的体积分为是
即为几何体(1)的体积分为是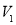 。(II) 作
。(II) 作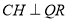 于点
于点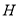 ,连结
,连结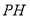 ,可证得
,可证得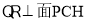 ,再得
,再得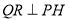 ,根据二面角平面角的定义可知
,根据二面角平面角的定义可知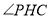 是二面角
是二面角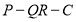 的平面角。最后在直角三角形
的平面角。最后在直角三角形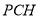 中求
中求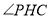 的正切值。
的正切值。
试题解析:解(I)设BC=a,则AB=2a,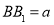 ,所以
,所以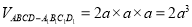 2分
2分
因为 4分
4分
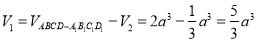 5分
5分
所以 6分
6分
(II)由点C作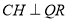 于点H,连结PH,因为
于点H,连结PH,因为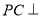 面CQR,
面CQR,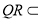 面CQR,所以
面CQR,所以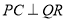
因为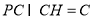 ,所以
,所以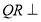 面PCH,又因为
面PCH,又因为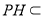 面PCH,
面PCH,
所以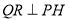 ,所以
,所以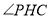 是二面角
是二面角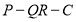 的平面角 9分
的平面角 9分
而
所以 12分
12分
考点:柱体、椎体的体积公式,二面角。

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目