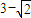题目内容
过双曲线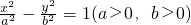
的右焦点F2作斜率为-1的直线，该直线与双曲线的两条渐近线的交点分别为A，B．若
，则双曲线的渐近线方程为
- A.3x±y=0
- B.x±3y=0
- C.2x±3y=0
- D.3x±2y=0
A
分析：由F2（c，0），知y=-x+c，渐近线y=
，y=-，由
，得A（
，
），由
，得B（
，
），所以|
|=
，|
|=
．由||=||，解得b=3a，由此能求出双曲线的渐近线方程．
解答：∵F2（c，0），∴y=-x+c，
渐近线y=，y=-，
由，得A（，），
由，得B（，），
∴||=
=，
||=
=．
∵||=||，∴
．
解得b=3a，
∴双曲线的渐近线方程为3x±y=0．
故选A．
点评：本题考查双曲线的性质和应用，解题时要认真审题，仔细解答，注意两点间距离公式的合理运用．
分析：由F2（c，0），知y=-x+c，渐近线y=
，y=-，由，得A（，），由，得B（，），所以||=，||=．由||=||，解得b=3a，由此能求出双曲线的渐近线方程．解答：∵F2（c，0），∴y=-x+c，
渐近线y=
，y=-，由
，得A（，），由
，得B（，），∴|
|==，|
|==．∵|
|=||，∴．解得b=3a，
∴双曲线的渐近线方程为3x±y=0．
故选A．
点评：本题考查双曲线的性质和应用，解题时要认真审题，仔细解答，注意两点间距离公式的合理运用．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
的右焦点F2的直线与右支交于A、B两点，且线段AF2、BF2的长度分别为m、n，m≥n.
，3]时，求
的取值范围.
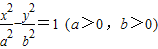的右焦点F2作斜率为-1的直线，该直线与双曲线的两条渐近线的交点分别为A，B．若
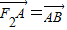，则双曲线的渐近线方程为（ ）
的右焦点F2，作倾斜角为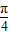
的直线交双曲线于A、B两点，
的右焦点F2作斜率为-1的直线，该直线与双曲线的两条渐近线的交点分别为A，B．若
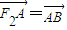，则双曲线的渐近线方程为（ ）
的右焦点F2作垂直于实轴的弦PQ，F1是左焦点，若∠PF1Q=90°，则双曲线的离心率是（ ）
