题目内容
袋子中放有大小和形状相同的小球若干个,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个.已知从袋子中随机抽取1个小球,取到标号是2的小球的概率是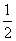 .
.
(1)求n的值;
(2)从袋子中不放回地随机抽取两个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.
①设事件A表示“a+b=2”,求事件A的概率;
②在区间[0,2]内任取两个实数x、y,求事件“x2+y2>(a-b)2恒成立”的概率.
(1)由题意可知: =
=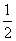 ,解得n=2.
,解得n=2.
(2)将标号为2的小球记作a1,a2
①两次不放回抽取小球的所有基本事件为:(0,1),(0,a1),(0,a2),(1,0),(1,a1),(1,a2),(a1,0),(a1,1),(a1,a2),(a2,0),(a2,1),(a2,a1),共12个,
事件A包含的基本事件为:(0,a1),(0,a2),(a1,0),(a2,0),共4个.
∴P(A)= =
= .
.
②记“x2+y2>(a-b)2恒成立”为事件B,则事件B等价于“x2+y2>4”,(x,y)可以看成平面中的点,
则全部结果所构成的区域Ω={(x,y)|0≤x≤2,0≤y≤2,x,y∈R},而事件B所构成的区域B={(x,y)|x2+y2>4,x,y∈Ω},
∴P(B)=

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
在2012年8月15日那天,某市物价部门对本市的5家商场的某商品的一天销售量及其价格进行调查,5家商场的售价x元和销售量y件之间的一组数据如下表所示:
| 价格x | 9 | 9.5 | m | 10.5 | 11 |
| 销售量y | 11 | n | 8 | 6 | 5 |
由散点图可知,销售量y与价格x之间有较强的线性相关关系,其线性回归直线方程是: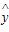 =-3.2x+40,且m+n=20,则其中的n=________.
=-3.2x+40,且m+n=20,则其中的n=________.

 B.
B.
 D.
D.
 的概率是( )
的概率是( ) B.
B.
 D.
D.