题目内容
5.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的中心在坐标原点O,对称轴在坐标轴上,椭圆的上顶点与两个焦点构成边长为2的正三角形.(1)求椭圆C的标准方程;
(2)若斜率为k的直线l经过点M(4,0),与椭圆C相交于A,B两点,且$\overrightarrow{OA}•\overrightarrow{OB}>\frac{1}{2}$,求k的取值范围.
分析 (1)由已知得2c=2,a=2,由此能求出椭圆C的标准方程.
(2)设直线l的方程为y=k(x-4),与椭圆联立,得((3+4k2)x2-32k2x+64k2-12=0,由此利用根的判别式、韦达定理、向量的数量积,能求出k的取值范围.
解答 解:(1)∵椭圆的上顶点与两个焦点构成边长为2的正三角形,
∴2c=2,a=2,∴b2=a2-c2=3
∴椭圆C的标准方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.…(4分)
(2)设直线l的方程为y=k(x-4),设A(x1,y1),B(x2,y2)
联立$\left\{\begin{array}{l}y=k(x-4)\\ 3{x^2}+4{y^2}=12\end{array}\right.$,消去y可得((3+4k2)x2-32k2x+64k2-12=0
∵直线l与椭圆C相交于A,B两点,∴△>0
由△=(32k2)2-4(3+4k2)(64k2-12)>0解得${k^2}<\frac{1}{4}$
设A(x1,y1),B(x2,y2)
则${x_1}+{x_2}=\frac{{32{k^2}}}{{4{k^2}+3}}$,${x_1}{x_2}=\frac{{64{k^2}-12}}{{4{k^2}+3}}$…(7分)
$\begin{array}{l}∵\overrightarrow{OA}•\overrightarrow{OB}={x_1}{x_2}+{y_1}{y_2}\\={x_1}{x_2}+k({x_1}-4)k({x_2}-4)\\=(1+{k^2}){x_1}{x_2}-4{k^2}({x_1}+{x_2})+16{k^2}\\=(1+{k^2})\frac{{64{k^2}-12}}{{3+4{k^2}}}-4{k^2}\frac{{32{k^2}}}{{3+4{k^2}}}+16{k^2}>\frac{1}{2}\end{array}$
解得${k^2}>\frac{27}{196}$∴$\frac{27}{196}<{k^2}<\frac{1}{4}$
∴k的取值范围是-$\frac{1}{2}<k<-\frac{3\sqrt{3}}{14}$或$\frac{3\sqrt{3}}{14}<k<\frac{1}{2}$.…(12分)
点评 本题考查椭圆的标准方程的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意根的判别式、韦达定理、向量的数量积的合理运用.

| A. | ±1 | B. | $±\frac{{\sqrt{2}}}{2}$ | C. | $±\frac{1}{2}$ | D. | $±\frac{1}{4}$ |
 已知五边形ABECD有一个直角梯形ABCD与一个等边三角形BCE构成,如图1所示,AB⊥BC,且AB=2BC=2CD,将梯形ABCD沿着BC折起,形成如图2所示的几何体,且AB⊥平面BEC.
已知五边形ABECD有一个直角梯形ABCD与一个等边三角形BCE构成,如图1所示,AB⊥BC,且AB=2BC=2CD,将梯形ABCD沿着BC折起,形成如图2所示的几何体,且AB⊥平面BEC. 如图,在四棱柱ABCD-A1B1C1D1中,AC⊥B1D,BB1⊥底面ABCD,E、F、H分别为AD、CD、DD1的中点,EF与BD交于点G.
如图,在四棱柱ABCD-A1B1C1D1中,AC⊥B1D,BB1⊥底面ABCD,E、F、H分别为AD、CD、DD1的中点,EF与BD交于点G.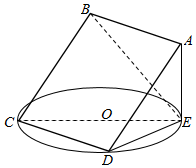 如图所示,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C,D的点,AE=3,圆O的直径为9.
如图所示,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C,D的点,AE=3,圆O的直径为9.