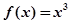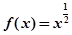题目内容
设函数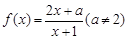 .
.
(1)用反证法证明:函数 不可能为偶函数;
不可能为偶函数;
(2)求证:函数 在
在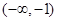 上单调递减的充要条件是
上单调递减的充要条件是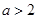 .
.
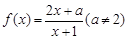 .
.(1)用反证法证明:函数
 不可能为偶函数;
不可能为偶函数;(2)求证:函数
 在
在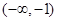 上单调递减的充要条件是
上单调递减的充要条件是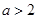 .
.(1)祥见解析;(2) 祥见解析.
试题分析:(1)反证法证明的一般步骤是:先假设结论不正确,从而肯定结论的反面一定成立,在此基础上结合题目已知条件,经过正确的推理论证得到一个矛盾,从而得到假设不成立,所以结论正确;此题只需假设假设函数
 是偶函数,既然是偶函数,则对定义域内的一切x都有
是偶函数,既然是偶函数,则对定义域内的一切x都有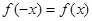 成立,那么我们为了说明假设不成立,即
成立,那么我们为了说明假设不成立,即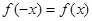 不可能成立,只需任取一个特殊值代入检验即可;(2)由于是证明函数
不可能成立,只需任取一个特殊值代入检验即可;(2)由于是证明函数 在
在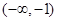 上单调递减的充要条件是:
上单调递减的充要条件是: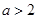 ;应分充分性和必要性两个方面来加以证明,先证充分性:
;应分充分性和必要性两个方面来加以证明,先证充分性: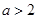 来证明
来证明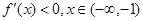 一定成立;再证必要性:由函数
一定成立;再证必要性:由函数 在
在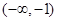 上单调递减
上单调递减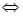
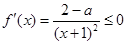 在
在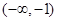 上恒成立,来证明
上恒成立,来证明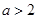 即可,注意已知中的
即可,注意已知中的 这一条件.
这一条件.试题解析:(1)假设函数
 是偶函数, 2分
是偶函数, 2分则
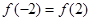 ,即
,即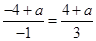 ,解得
,解得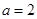 , 4分
, 4分这与
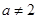 矛盾,所以函数
矛盾,所以函数 不可能是偶函数. 6分
不可能是偶函数. 6分(2)因为
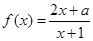 ,所以
,所以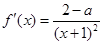 . 8分
. 8分①充分性:当
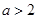 时,
时,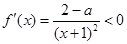 ,
,所以函数
 在
在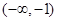 单调递减; 10分
单调递减; 10分②必要性:当函数
 在
在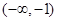 单调递减时,
单调递减时,有
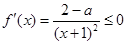 ,即
,即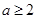 ,又
,又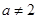 ,所以
,所以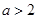 . 13分
. 13分综合①②知,原命题成立. 14分
(说明:用函数单调性的定义证明的,类似给分;用反比例函数图象说理的,适当扣分)

练习册系列答案
相关题目
 .
. 的定义域;
的定义域; 时,函数
时,函数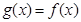 ,求函数
,求函数 的值域.
的值域.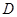 的函数
的函数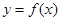 ,若同时满足:
,若同时满足: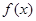 在
在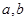 ]
]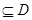 ,使
,使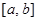 上的值域为
上的值域为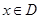 )叫做闭函数.
)叫做闭函数.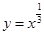 符合条件②的区间
符合条件②的区间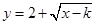 是闭函数,求实数
是闭函数,求实数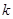 的取值范围.
的取值范围.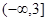 上
上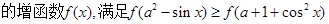 对一切实数x恒成立,求实数a的取值范围。
对一切实数x恒成立,求实数a的取值范围。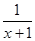
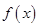 在
在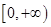 单调递减,
单调递减,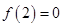 .若
.若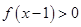 ,则
,则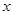 的取值范围是__________.
的取值范围是__________. 的单调递减函数是( )
的单调递减函数是( )