题目内容
对于定义域为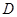 的函数
的函数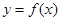 ,若同时满足:
,若同时满足:
①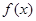 在
在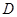 内单调递增或单调递减;
内单调递增或单调递减;
②存在区间[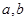 ]
]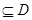 ,使
,使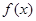 在
在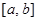 上的值域为
上的值域为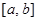 ;
;
那么把函数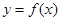 (
(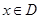 )叫做闭函数.
)叫做闭函数.
(1) 求闭函数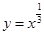 符合条件②的区间
符合条件②的区间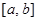 ;
;
(2) 若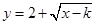 是闭函数,求实数
是闭函数,求实数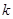 的取值范围.
的取值范围.
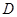 的函数
的函数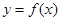 ,若同时满足:
,若同时满足:①
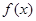 在
在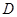 内单调递增或单调递减;
内单调递增或单调递减;②存在区间[
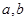 ]
]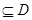 ,使
,使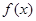 在
在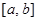 上的值域为
上的值域为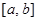 ;
;那么把函数
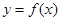 (
(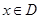 )叫做闭函数.
)叫做闭函数.(1) 求闭函数
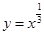 符合条件②的区间
符合条件②的区间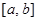 ;
;(2) 若
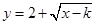 是闭函数,求实数
是闭函数,求实数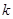 的取值范围.
的取值范围.(1)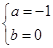 或
或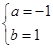 或
或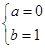 ,(2)
,(2)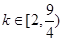 .
.
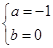 或
或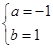 或
或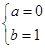 ,(2)
,(2)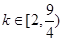 .
.试题分析:(1)新定义的问题,首先按新定义进行等价转化. 由题意,
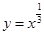 在[
在[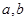 ]上递增,则
]上递增,则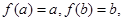
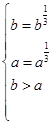 解得
解得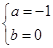 或
或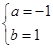 或
或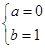 ,(2)若
,(2)若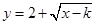 是闭函数,则存在区间[
是闭函数,则存在区间[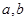 ],在区间[
],在区间[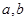 ]上,函数
]上,函数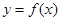 的值域为[
的值域为[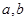 ],可证明函数
],可证明函数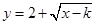 在定义域内单调递增,因此
在定义域内单调递增,因此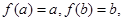 ∴
∴ 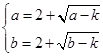 ∴
∴ 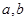 为方程
为方程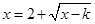 的两个实数根. 即方程
的两个实数根. 即方程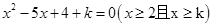 有两个不相等的实根.
有两个不相等的实根. 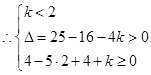 或
或 解得
解得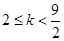 ,综上所述,
,综上所述,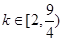
试题解析:[解析](1)由题意,
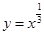 在[
在[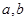 ]上递增,则
]上递增,则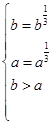 ,
,解得
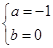 或
或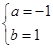 或
或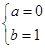
所以,所求的区间为[-1,0]或[-1,1]或[0,1] . 6分(解得一个区间得2分)
(2)若
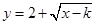 是闭函数,则存在区间[
是闭函数,则存在区间[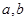 ],在区间[
],在区间[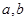 ]上,
]上,函数
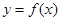 的值域为[
的值域为[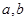 ] 6分
] 6分容易证明函数
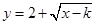 在定义域内单调递增,
在定义域内单调递增,∴
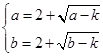 8分
8分∴
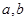 为方程
为方程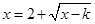 的两个实数根. 10分
的两个实数根. 10分即方程
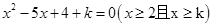 有两个不相等的实根.
有两个不相等的实根. 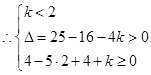 或
或 14分
14分解得
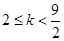 ,综上所述,
,综上所述,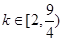 16分
16分 
练习册系列答案
相关题目
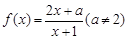 .
. 不可能为偶函数;
不可能为偶函数; 上单调递减的充要条件是
上单调递减的充要条件是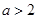 .
.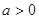 且
且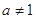 ,函数
,函数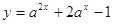 在
在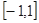 的最大值是14,求
的最大值是14,求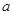 的值。
的值。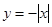 奇偶性相同且在(-∞,0)上单调性也相同的是( ).
奇偶性相同且在(-∞,0)上单调性也相同的是( ).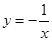
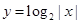
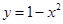
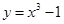
 在区间
在区间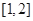 上的最小值是( )
上的最小值是( )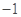
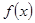 是定义在
是定义在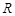 上的偶函数,且在区间
上的偶函数,且在区间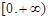 上是单调增函数.如果实数
上是单调增函数.如果实数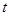 满足
满足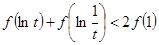 ,则
,则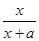 在(-2,+∞)上为增函数,则a的取值范围是________.
在(-2,+∞)上为增函数,则a的取值范围是________.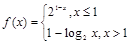 ,则满足
,则满足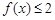 的x的取值范围是 .
的x的取值范围是 .