题目内容
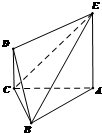 如图,五面体ABCDE中,正△ABC的边长为1,AE⊥平面ABC,CD∥AE,且CD=
如图,五面体ABCDE中,正△ABC的边长为1,AE⊥平面ABC,CD∥AE,且CD=| 1 |
| 2 |
(I)设CE与平面ABE所成的角为α,AE=k(k>0),若α∈[
| π |
| 6 |
| π |
| 4 |
(Ⅱ)在(I)和条件下,当k取得最大值时,求平面BDE与平面ABC所成角的大小.
分析:(Ⅰ)建立空间直角坐标系(如图),表示出点的坐标,确定平面ABE的一个法向量,利用CE与平面ABE所成的角,且α∈[
,
],即可求k的取值范围;
(Ⅱ)由(Ⅰ)知k最大值为
,则当k=
时,求出平面BDE法向量
=(-
,-1,
),平面ABC法向量为
=(0,0,1),利用夹角公式,即可求得平面BDE与平面ABC所成角大小.
| π |
| 6 |
| π |
| 4 |
(Ⅱ)由(Ⅰ)知k最大值为
| 2 |
| 2 |
| n |
| 3 |
| 2 |
| m |
解答: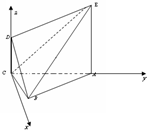 解:(Ⅰ)如图以C为坐标原点,CA、CD为y、z轴,垂直于CA、CD的直线CT为x轴,建立空间直角坐标系(如图),则设A(0,1,0),D(0,0,
解:(Ⅰ)如图以C为坐标原点,CA、CD为y、z轴,垂直于CA、CD的直线CT为x轴,建立空间直角坐标系(如图),则设A(0,1,0),D(0,0,
),E(0,1,k),B(
,
,0).
取AB的中点M,则M(
,
,0),则平面ABE的一个法向量为
=(
,
,0),
由题意sinα=
=
=
.
由α∈[
,
],则
≤sinα=
≤
,
得
≤k≤
.…6分
(Ⅱ)由(Ⅰ)知k最大值为
,则当k=
时,设平面BDE法向量为
=(x,y,z),则
取
=(-
,-1,
),又平面ABC法向量为
=(0,0,1),…10分
所以cos<
,
>=
=
,
所以平面BDE与平面ABC所成角大小arccos
.…12分.
 解:(Ⅰ)如图以C为坐标原点,CA、CD为y、z轴,垂直于CA、CD的直线CT为x轴,建立空间直角坐标系(如图),则设A(0,1,0),D(0,0,
解:(Ⅰ)如图以C为坐标原点,CA、CD为y、z轴,垂直于CA、CD的直线CT为x轴,建立空间直角坐标系(如图),则设A(0,1,0),D(0,0,| k |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
取AB的中点M,则M(
| ||
| 4 |
| 3 |
| 4 |
| CM |
| ||
| 4 |
| 3 |
| 4 |
由题意sinα=
| ||||
|
| ||||||||
|
| ||
2
|
由α∈[
| π |
| 6 |
| π |
| 4 |
| 1 |
| 2 |
| ||
2
|
| ||
| 2 |
得
| ||
| 2 |
| 2 |
(Ⅱ)由(Ⅰ)知k最大值为
| 2 |
| 2 |
| n |
|
取
| n |
| 3 |
| 2 |
| m |
所以cos<
| n |
| m |
| ||
|
| ||
| 3 |
所以平面BDE与平面ABC所成角大小arccos
| ||
| 3 |
点评:本题考查利用空间向量解决立体几何问题,解题的关键是建立空间直角坐标系,正确运用向量的数量积公式,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
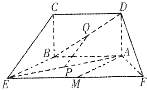 如图,五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,
如图,五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,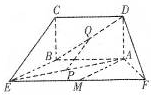 如图,五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,AB=
如图,五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,AB=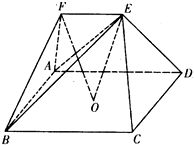 (2013•临沂一模)如图,五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面ABF是等边三角形,棱EF∥BC,且EF=
(2013•临沂一模)如图,五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面ABF是等边三角形,棱EF∥BC,且EF=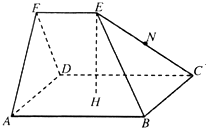 (2012•湛江二模)如图,五面体ABCD中,ABCD是以点H为中心的正方形,EF∥AB,EH丄平面ABCD,AB=2,EF=EH=1.
(2012•湛江二模)如图,五面体ABCD中,ABCD是以点H为中心的正方形,EF∥AB,EH丄平面ABCD,AB=2,EF=EH=1.