题目内容
如图,五面体ABCD中,ABCD是以点H为中心的正方形,EF∥AB,EH丄平面ABCD,AB=2,EF=EH=1.(1)证明:平面ADF丄平面ABCD;
(2)求五面体EF-ABCD的体积;
(3)设N为EC的中点,若在平面ABCD内存在一点M,使MN丄平面BCE,求MN的长.

【答案】分析:(1)取AD的中点G,连接BD、GH、GF,利用正方形的性质结合三角形中位线定理,可证出四边形EFGH为平行四边形,从而EH∥FG,结合EH⊥平面ABCD,得到FG⊥平面ABCD,最后根据面面垂直的判定定理,得到平面ADF丄平面ABCD;
(2)在平面ABCD内过点H作直线IJ∥AD,分别交AB、CD于I、J.由(1)的证明过程,可得三棱柱ADF-IJE是直三棱柱,从而得到它的体积为:S△IJE×EF= IJ×EH×EF=1.又因为四棱锥E-IJCB的体积为:
IJ×EH×EF=1.又因为四棱锥E-IJCB的体积为: SIJCB×EH=
SIJCB×EH= ,相加即得五面体EF-ABCD的体积.
,相加即得五面体EF-ABCD的体积.
(3)以G为原点,AD所在直线为x轴,建立如图坐标系,分别得出B、C、E、N各点的坐标,设M(x,y,0),若MN⊥平面BCE,则MN⊥EB且MN⊥EC,利用向量数量积为0,联列方程组,解之得x= ,y=1.从而得到向量
,y=1.从而得到向量 的坐标,利用向量模的公式,可得MN的长.
的坐标,利用向量模的公式,可得MN的长.
解答:解:(1)由题意,得:EF∥AB,且EF= AB,
AB,
取AD的中点G,连接BD、GH、GF,
∵H是正方形ABCD的中心,
∴H是BD的中点,得到△ABD中,GH是中位线,
∴GH∥AB,GH= AB,
AB,
∴EF∥GH且EF=GH,可得四边形EFGH为平行四边形,
∴EH∥FG,
又∵EH⊥平面ABCD,∴FG⊥平面ABCD,
∵FG?平面ADF,∴平面ADF丄平面ABCD;
(2)在平面ABCD内过点H作直线IJ∥AD,分别交AB、CD于I、J.
由(1)的证明过程,得EF∥AI∥DJ,且EF=AI=DJ=1
∵EF⊥平面ADF,∴三棱柱ADF-IJE是直三棱柱
∴V三棱柱ADF-IJE=S△IJE×EF= IJ×EH×EF=
IJ×EH×EF= ×2×1×1=1.
×2×1×1=1.
又∵V四棱锥E-IJCB= SIJCB×EH=
SIJCB×EH= ×
× SABCD×EH=
SABCD×EH= .
.
∴五面体EF-ABCD的体积为V=V三棱柱ADF-IJE+V四棱锥E-IJCB=1+ =
= .
.
(3)以G为原点,AD所在直线为x轴,建立如图坐标系,则
B(1,2,0),C(-1,2,0),E(0,1,1),N(- ,
, ,
, ),
),
设M(x,y,0),可得 ,
, ,
,
若MN⊥平面BCE,则 ,
,
解之得:x= ,y=1.
,y=1.
∴向量 ,
,
因此 =
= =
=
点评:本题给出一个由直三棱柱和四棱锥拼接而成的五面体,通过证明面面垂直和求体积,着重考查了组合几何体的体积公式,以及平面与平面垂直的判定等知识点,属于中档题.
(2)在平面ABCD内过点H作直线IJ∥AD,分别交AB、CD于I、J.由(1)的证明过程,可得三棱柱ADF-IJE是直三棱柱,从而得到它的体积为:S△IJE×EF=
 IJ×EH×EF=1.又因为四棱锥E-IJCB的体积为:
IJ×EH×EF=1.又因为四棱锥E-IJCB的体积为: SIJCB×EH=
SIJCB×EH= ,相加即得五面体EF-ABCD的体积.
,相加即得五面体EF-ABCD的体积.(3)以G为原点,AD所在直线为x轴,建立如图坐标系,分别得出B、C、E、N各点的坐标,设M(x,y,0),若MN⊥平面BCE,则MN⊥EB且MN⊥EC,利用向量数量积为0,联列方程组,解之得x=
 ,y=1.从而得到向量
,y=1.从而得到向量 的坐标,利用向量模的公式,可得MN的长.
的坐标,利用向量模的公式,可得MN的长.解答:解:(1)由题意,得:EF∥AB,且EF=
 AB,
AB,
取AD的中点G,连接BD、GH、GF,
∵H是正方形ABCD的中心,
∴H是BD的中点,得到△ABD中,GH是中位线,
∴GH∥AB,GH=
 AB,
AB,∴EF∥GH且EF=GH,可得四边形EFGH为平行四边形,
∴EH∥FG,
又∵EH⊥平面ABCD,∴FG⊥平面ABCD,

∵FG?平面ADF,∴平面ADF丄平面ABCD;
(2)在平面ABCD内过点H作直线IJ∥AD,分别交AB、CD于I、J.
由(1)的证明过程,得EF∥AI∥DJ,且EF=AI=DJ=1
∵EF⊥平面ADF,∴三棱柱ADF-IJE是直三棱柱
∴V三棱柱ADF-IJE=S△IJE×EF=
 IJ×EH×EF=
IJ×EH×EF= ×2×1×1=1.
×2×1×1=1.又∵V四棱锥E-IJCB=
 SIJCB×EH=
SIJCB×EH= ×
× SABCD×EH=
SABCD×EH= .
.∴五面体EF-ABCD的体积为V=V三棱柱ADF-IJE+V四棱锥E-IJCB=1+
 =
= .
.
(3)以G为原点,AD所在直线为x轴,建立如图坐标系,则
B(1,2,0),C(-1,2,0),E(0,1,1),N(-
 ,
, ,
, ),
),设M(x,y,0),可得
 ,
, ,
,
若MN⊥平面BCE,则
 ,
,解之得:x=
 ,y=1.
,y=1.∴向量
 ,
,因此
 =
= =
=
点评:本题给出一个由直三棱柱和四棱锥拼接而成的五面体,通过证明面面垂直和求体积,着重考查了组合几何体的体积公式,以及平面与平面垂直的判定等知识点,属于中档题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 如图,五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,
如图,五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF, 如图,五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,AB=
如图,五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,AB= (2013•临沂一模)如图,五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面ABF是等边三角形,棱EF∥BC,且EF=
(2013•临沂一模)如图,五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面ABF是等边三角形,棱EF∥BC,且EF=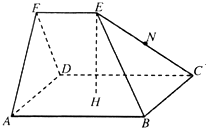 (2012•湛江二模)如图,五面体ABCD中,ABCD是以点H为中心的正方形,EF∥AB,EH丄平面ABCD,AB=2,EF=EH=1.
(2012•湛江二模)如图,五面体ABCD中,ABCD是以点H为中心的正方形,EF∥AB,EH丄平面ABCD,AB=2,EF=EH=1.