题目内容
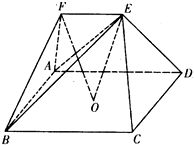 (2013•临沂一模)如图,五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面ABF是等边三角形,棱EF∥BC,且EF=
(2013•临沂一模)如图,五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面ABF是等边三角形,棱EF∥BC,且EF=| 1 | 2 |
(I)证明:EO∥面ABF;
(Ⅱ)若EF=EO,证明:平面EFO⊥平面ABE.
分析:(I)通过证平行四边形证线线平行,再由线线平行证明线面平行即可;
(II)先通过证线面垂直证线线垂直,再由线线垂直⇒线面垂直⇒面面垂直.
(II)先通过证线面垂直证线线垂直,再由线线垂直⇒线面垂直⇒面面垂直.
解答:证明:(I)证明:取AB的中点M,连接FM,OM,
∵O为矩形ABCD的对角线的交点,∴OM∥BC,且OM=
BC,
又EF∥BC,且EF=
BC,∴OM=EF,且EF∥OM,
∴四边形EFMO为平行四边形,∴EO∥FM,又FM?平面ABF,EO?平面ABF,
∴EO∥平面ABF.
(II)∵由(I)知四边形EFMO为平行四边形,∵EE=EO,
∴四边形EFMO为菱形,连接EM,则FO⊥EM,
又∵三角形ABF为等边三角形,且M为AB的中点,
∴FM⊥AB,MO⊥AB,∴AB⊥平面EFMO,∴AB⊥FO,
又AB∩EM=M,∴FO⊥平面ABE,FO?平面EFO,
∴平面ABE⊥平面EFO.
∵O为矩形ABCD的对角线的交点,∴OM∥BC,且OM=
| 1 |
| 2 |
又EF∥BC,且EF=
| 1 |
| 2 |

∴四边形EFMO为平行四边形,∴EO∥FM,又FM?平面ABF,EO?平面ABF,
∴EO∥平面ABF.
(II)∵由(I)知四边形EFMO为平行四边形,∵EE=EO,
∴四边形EFMO为菱形,连接EM,则FO⊥EM,
又∵三角形ABF为等边三角形,且M为AB的中点,
∴FM⊥AB,MO⊥AB,∴AB⊥平面EFMO,∴AB⊥FO,
又AB∩EM=M,∴FO⊥平面ABE,FO?平面EFO,
∴平面ABE⊥平面EFO.
点评:本题考查线面平行的判定及面面垂直的判定.

练习册系列答案
相关题目
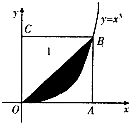 (2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
(2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )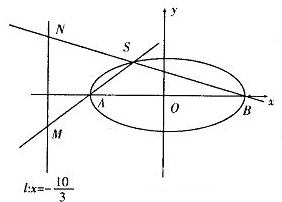 (2013•临沂一模)如图,已知椭圆C:
(2013•临沂一模)如图,已知椭圆C: