题目内容
某出租车公司计划用450万元购买A型和B型两款汽车投入营运,购买总量不超过50辆,其中购买A型汽车需要13万元/辆,购买B型汽车需要8万元/辆,假设公司第一年A型汽车的纯利润为5万元/辆,B型汽车的纯利润为1.5万元/辆,为使该公司第一年纯利润最大,则需安排购买( )
| A.8辆A型汽车,42辆B型汽车 | B.9辆A型汽车,41辆B型汽车 |
| C.11辆A型汽车,39辆B型汽车 | D.10辆A型汽车,40辆B型汽车 |
D
解析试题分析:解法一: 时,成本为
时,成本为 万元,利润为
万元,利润为 万元;
万元; 时,成本为
时,成本为 万元,利润为
万元,利润为 万元;
万元; 时,成本为
时,成本为 万元,利润为
万元,利润为 万元;
万元;
而 ,选
,选 .
.
解法二:设购买 型出租车x辆,购买
型出租车x辆,购买 型出租车
型出租车 辆,第一年纯利润为
辆,第一年纯利润为 ,则
,则
 ,作出可行域,由
,作出可行域,由 解得
解得 ,此时z取得最大值,选
,此时z取得最大值,选 .
.
考点:线性规划问题.

练习册系列答案
相关题目
不等式组 表示的平面区域是( )
表示的平面区域是( )
| A.矩形 | B.三角形 | C.直角梯形 | D.等腰梯形 |
已知变量 满足约束条件
满足约束条件 ,则
,则 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
已知实数x,y满足 ,则目标函数z=x-y的最小值为( )
,则目标函数z=x-y的最小值为( )
| A.-2 | B.5 | C.6 | D.7 |
在圆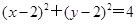 内任取一点,则该点恰好在区域
内任取一点,则该点恰好在区域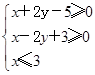 内的概率为( )
内的概率为( )
A.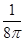 | B.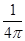 | C.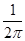 | D.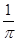 |
已设变量 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最大值为( )
的最大值为( )
| A.11 | B.10 | C.9 | D. |
不等式 表示的区域在直线
表示的区域在直线 的( )
的( )
| A.右上方 | B.右下方 | C.左上方 | D.左下方 |
已知 满足不等式组
满足不等式组 ,则
,则 的最大值除以最小值等于( )
的最大值除以最小值等于( )
A.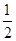 | B.2 | C. | D.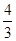 |
 表示的平面区域为
表示的平面区域为 .若圆
.若圆
 不经过区域
不经过区域 的取值范围是( )
的取值范围是( )


