题目内容
设f(x)=cos22x,则f′(
)=( )
| π |
| 8 |
| A、2 | ||
B、
| ||
| C、-1 | ||
| D、-2 |
分析:先对函数进行化简,再对函数进行求导,再把x=
代入进行求解即可.
| π |
| 8 |
解答:解:∵f(x)=cos22x=
+
cos4x
∴f′(x)=
(cos4x)′(4x)′=-2sin4x
∴f′(
)=-2sin
=-2
故选D.
| 1 |
| 2 |
| 1 |
| 2 |
∴f′(x)=
| 1 |
| 2 |
∴f′(
| π |
| 8 |
| π |
| 2 |
故选D.
点评:本题主要考查了复合函数的求导问题,要注意{f[g(x)]}′=f′(g(x)g′(x).

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
 sinωxcosωx
sinωxcosωx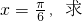 ω的值.
ω的值. sinωxcosωx
sinωxcosωx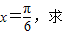 ω的值.
ω的值.