题目内容
已知角α是锐角，求sinα+| 3 |
分析：化简sinα+
cosα为2sin（α+
），根据2sin（α+
）的范围，求出sinα+
cosα的范围．
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
解答：解：sinα+
cosα=2（
sinα+
cosα）=2sin（α+
）
因为角α是锐角，sin（α+
）∈[
， 1]
所以sinα+
cosα∈[
，2]
故答案为：[
，2]
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
因为角α是锐角，sin（α+
| π |
| 3 |
| ||
| 2 |
所以sinα+
| 3 |
| 3 |
故答案为：[
| 3 |
点评：本题考查正弦函数的定义域和值域，考查运算能力，是基础题．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
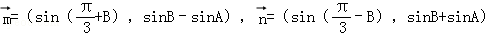，若
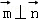
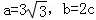，求三角形面积S△ABC．
，若
，求三角形面积S△ABC．
，求b的值。
，求b的值。