题目内容
2010年广州亚运会的一组志愿者全部通晓中文,并且每个志愿者还都通晓英语、日语和韩语中的一种(但无人通晓两种外语),已知从中任抽一人,其通晓中文和英语的概率为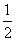 ,通晓中文和日语的概率为
,通晓中文和日语的概率为 .若通晓中文和韩语的人数不超过3人.
.若通晓中文和韩语的人数不超过3人.
(1)求这组志愿者的人数;
(2)现从这组志愿者中选出通晓英语的志愿者1名,通晓韩语的志愿者1名,若甲通晓英语,乙通晓韩语,求甲和乙不全被选中的概率.
解析:(1)设通晓中文和英语的人数为x人,通晓中文和日语的人数为y人,通晓中文和韩语的人数为z人,且x,y,z∈N*,则
 且0<z≤3,
且0<z≤3,
依题意则有:
所以这组志愿者的人数为5+3+2=10.
(2)设通晓中文和英语的 人为A1,A2,A3,A4,A5,甲为A1,通晓中文和韩语的人为B1,B2,乙为B1,则从这组志愿者中选出通晓英语和韩语的志愿者各1名的所有情况为:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(A5,B1),(A5,B2),共10个,
人为A1,A2,A3,A4,A5,甲为A1,通晓中文和韩语的人为B1,B2,乙为B1,则从这组志愿者中选出通晓英语和韩语的志愿者各1名的所有情况为:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(A5,B1),(A5,B2),共10个,
同时选中甲、乙只有(A1,B1)1个.
所以甲和乙不全被选中的概率为1- =
= .
.

练习册系列答案
相关题目
从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:
| 分组(重量) | [80,85) | [85,90) | [90,95) | [95,100) |
| 频数(个) | 5 | 10 | 20 | 15 |
(1)根据频数分布表计算苹果的重量在[90,95)的频率;
(2)用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[ 95,100)中各有1个的概率.
95,100)中各有1个的概率.
 (k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2012年生产该产品的固
(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2012年生产该产品的固 定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金). 的概率是( )
的概率是( ) 
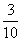 B.
B. C.
C.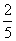 D.
D.
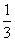
 ,则下列说法正确的是( )
,则下列说法正确的是( ) B.甲不输的概率是
B.甲不输的概率是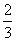 D.乙不输的概率是
D.乙不输的概率是 B.
B. C.
C. D.
D.
 组数据中的每一个数据都乘以2,再都减去80,得
组数据中的每一个数据都乘以2,再都减去80,得