题目内容
(本小题满分13分)设函数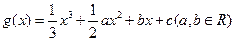 的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为
的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为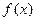 .
.
(1)若方程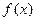 =0有两个实根分别为-2和4,求
=0有两个实根分别为-2和4,求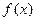 的表达式;
的表达式;
(2)若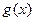 在区间[-1,3]上是单调递减函数,求
在区间[-1,3]上是单调递减函数,求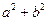 的最小值.
的最小值.
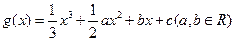 的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为
的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为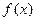 .
.(1)若方程
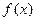 =0有两个实根分别为-2和4,求
=0有两个实根分别为-2和4,求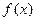 的表达式;
的表达式;(2)若
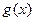 在区间[-1,3]上是单调递减函数,求
在区间[-1,3]上是单调递减函数,求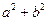 的最小值.
的最小值.(Ⅰ)因为函数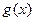 的图象经过原点,所以
的图象经过原点,所以 ,则
,则 .
.
根据导数的几何意义知 ,………4分
,………4分
由已知—2、4是方程 的两个实数,
的两个实数,
由韦达定理, …………6分
…………6分
(Ⅱ)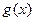 在区间[—1,3]上是单调减函数,所以在[—1,3]区间上恒有
在区间[—1,3]上是单调减函数,所以在[—1,3]区间上恒有
 ,即
,即 在[—1,3]恒成立,
在[—1,3]恒成立,
这只需满足 即可,也即
即可,也即 …………10分
…………10分
而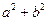 可视为平面区域
可视为平面区域 内的点到原点距离的平方,其中点(—2,—3)距离原点最近,
内的点到原点距离的平方,其中点(—2,—3)距离原点最近,
所以当 时,
时, 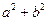 有最小值13…………13分
有最小值13…………13分
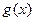 的图象经过原点,所以
的图象经过原点,所以 ,则
,则 .
.根据导数的几何意义知
 ,………4分
,………4分由已知—2、4是方程
 的两个实数,
的两个实数,由韦达定理,
 …………6分
…………6分(Ⅱ)
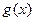 在区间[—1,3]上是单调减函数,所以在[—1,3]区间上恒有
在区间[—1,3]上是单调减函数,所以在[—1,3]区间上恒有 ,即
,即 在[—1,3]恒成立,
在[—1,3]恒成立,这只需满足
 即可,也即
即可,也即 …………10分
…………10分而
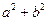 可视为平面区域
可视为平面区域 内的点到原点距离的平方,其中点(—2,—3)距离原点最近,
内的点到原点距离的平方,其中点(—2,—3)距离原点最近,所以当
 时,
时, 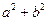 有最小值13…………13分
有最小值13…………13分略

练习册系列答案
相关题目
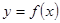 的图象与
的图象与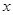 轴围成的阴影部分面积,用定积分可表示为
轴围成的阴影部分面积,用定积分可表示为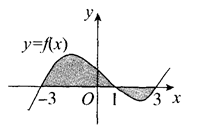
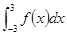

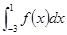
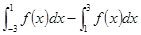
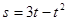 ,其中位移s单位为米,时间t的单
,其中位移s单位为米,时间t的单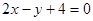 平行的抛物线
平行的抛物线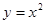 的切线方程是
的切线方程是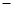 y+3=0
y+3=0 .
.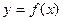 在点
在点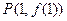 处的切线与直线
处的切线与直线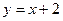 垂直,求函数
垂直,求函数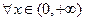 都有
都有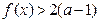 成立,试求
成立,试求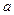 的取值范围;
的取值范围;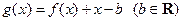 .当
.当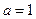 时,函数
时,函数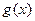 在区间
在区间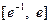 上有两个零点,求实数
上有两个零点,求实数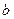 的取值范围.
的取值范围. 在点
在点 处的切线方程为 .
处的切线方程为 . 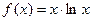
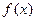 的最小值;
的最小值;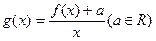 的单调区间;
的单调区间;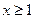 时,
时,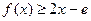 成立。
成立。 在点
在点 处的切线与
处的切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,则
,则 的值为
的值为 

