题目内容
两个分类变量X和Y,值域分别为{x1,x2}和{y1,y2},其样本频数分别是a=10,b=21.c+d=35,若判断变量X和Y有关错误频率不超过25%,则c等于( )
| A、3 | B、4 | C、5 | D、6 |
考点:相关系数
专题:概率与统计
分析:根据随机变量的2×2列联表,以及独立检验随机变量K2的临界值参考表,计算K2对应的值,验证c=3、4、5、6,K2是否恰好满足大于或等于1.323即可.
解答:
解:根据随机变量的2×2列联表,
以及独立检验随机变量K2的临界值参考表:
计算K2=
=
,其中n=a+b+c+d为样本容量;
∴当c=3时,K2=
≈4.9056>3.841,对应的P=0.05,即不超过5%的出错率,∴A不合题意;
当c=4时,K2=
≈3.579>2.706,对应的P=0.10,即不超过10%的出错率,∴B不合题意;
当c=5时,K2=
≈2.528>2.072,对应的P=0.15,即不超过15%的出错率,∴C不合题意;
当c=6时,K2=
≈1.704>1.323,对应的P=0.25,即不超过25%的出错率,∴D满足题意.
故选:D.
| y1 | y2 | 合计 | |
| x1 | 10 | 21 | 31 |
| x2 | c | 35-c | 35 |
| 合计 | 10+c | 66-c | 66 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 66(10(35-c)-21c)2 |
| 31×35×(10+c)×(66-c) |
∴当c=3时,K2=
| 66(10×32-63)2 |
| 31×35×13×63 |
当c=4时,K2=
| 66×(310-84)2 |
| 31×35×14×62 |
当c=5时,K2=
| 66×(300-105)2 |
| 31×35×15×61 |
当c=6时,K2=
| 66×(290-126)2 |
| 31×35×16×60 |
故选:D.
点评:本题考查了随机变量的2×2列联表以及独立检验随机变量K2的应用问题,是基础题目.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
函数f(x)=sinxsin(
+x)-x的零点的个数为( )
| π |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
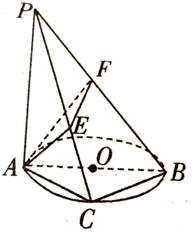 如图,AB是圆O的直径,C为圆周上一点,PA⊥平面ABC,若AE⊥PC,F是PD上任意一点,求证:平面AEF⊥平面PBC.
如图,AB是圆O的直径,C为圆周上一点,PA⊥平面ABC,若AE⊥PC,F是PD上任意一点,求证:平面AEF⊥平面PBC.