题目内容
函数f（x）=Asin（2x+φ）（A，φ∈R）的部分图象如图所示，那么f（0）=
- A.-
- B.-
- C.-1
- D.-
C
分析：先由图象中所给的数据确定函数的解析式，再计算f（0）的值．
解答：由题意，A=2，
∴f（x）=2sin（2x+φ）
将点（
，2）代入函数解析式，可得2sin（2×+φ）=2，
∴φ=2kπ-
（k∈Z）
∴f（0）=2sinφ=-1
故选C．
点评：本题考查三角函数的图象与解析式，解题的关键是读懂图象，求得函数的解析式．
分析：先由图象中所给的数据确定函数的解析式，再计算f（0）的值．
解答：由题意，A=2，
∴f（x）=2sin（2x+φ）
将点（
，2）代入函数解析式，可得2sin（2×+φ）=2，∴φ=2kπ-
（k∈Z）∴f（0）=2sinφ=-1
故选C．
点评：本题考查三角函数的图象与解析式，解题的关键是读懂图象，求得函数的解析式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，是函数f（x）=Asin（φx+φ）（其中A＞0，φ＞0，0＜φ＜π）的部分图象，则其解析为
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜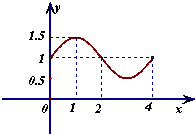
函数f（x）=Asin（ωx+φ）+b的图象如图，则f（x）的解析式和S=f（0）+f（1）+f（2）+…+f（2008）的值分别为（ ）