题目内容
点P在椭圆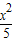 +
+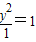 上,F1,F2为焦点 且∠F1PF2=60°,则△F1PF2的面积为( )
上,F1,F2为焦点 且∠F1PF2=60°,则△F1PF2的面积为( )A.
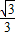
B.4
C.
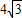
D.
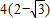
【答案】分析:由点P在椭圆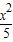 +
+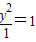 上,F1,F2为焦点 且∠F1PF2=60°,利用椭圆性质和余弦定理,建立方程组,求出|PF1|•|PF2|=
上,F1,F2为焦点 且∠F1PF2=60°,利用椭圆性质和余弦定理,建立方程组,求出|PF1|•|PF2|= ,再由正弦定理能够求出△F1PF2的面积.
,再由正弦定理能够求出△F1PF2的面积.
解答:解:∵点P在椭圆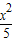 +
+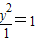 上,F1,F2为焦点 且∠F1PF2=60°,
上,F1,F2为焦点 且∠F1PF2=60°,
∴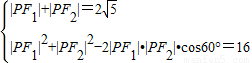 ,
,
解得|PF1|•|PF2|= ,
,
∴△F1PF2的面积S=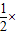 |PF1|•|PF2|•sin60°=
|PF1|•|PF2|•sin60°=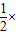
 ×
×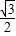 =
=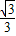 .
.
故选A.
点评:若点P在椭圆上,F1,F2为焦点 且∠F1PF2=θ,则△F1PF2的面积为S=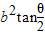 .
.
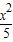 +
+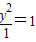 上,F1,F2为焦点 且∠F1PF2=60°,利用椭圆性质和余弦定理,建立方程组,求出|PF1|•|PF2|=
上,F1,F2为焦点 且∠F1PF2=60°,利用椭圆性质和余弦定理,建立方程组,求出|PF1|•|PF2|= ,再由正弦定理能够求出△F1PF2的面积.
,再由正弦定理能够求出△F1PF2的面积.解答:解:∵点P在椭圆
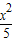 +
+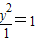 上,F1,F2为焦点 且∠F1PF2=60°,
上,F1,F2为焦点 且∠F1PF2=60°,∴
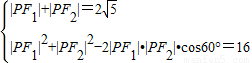 ,
,解得|PF1|•|PF2|=
 ,
,∴△F1PF2的面积S=
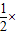 |PF1|•|PF2|•sin60°=
|PF1|•|PF2|•sin60°=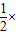
 ×
×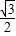 =
=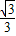 .
.故选A.
点评:若点P在椭圆上,F1,F2为焦点 且∠F1PF2=θ,则△F1PF2的面积为S=
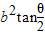 .
. 
练习册系列答案
相关题目
 +
+ =1上,F1,F2是椭圆的焦点,若
=1上,F1,F2是椭圆的焦点,若 为钝角,则P点的横坐标的取值范围是
为钝角,则P点的横坐标的取值范围是
 +
+ =1上,F1,F2是椭圆的焦点,若∠F1PF2为钝角,则P点的横坐标的取值范围是________.
=1上,F1,F2是椭圆的焦点,若∠F1PF2为钝角,则P点的横坐标的取值范围是________. +
+ =1上,F1,F2是椭圆的焦点,若∠F1PF2为钝角,则P点的横坐标的取值范围是 .
=1上,F1,F2是椭圆的焦点,若∠F1PF2为钝角,则P点的横坐标的取值范围是 .