题目内容
已知椭圆C的中心为原点O,点F2(1,0)是它的一个焦点,直线l过点F2与椭圆C交于A,B两点,当直线l垂直于x轴时,△OAB的面积S△OAB=
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点P在椭圆C上,F1,F2是椭圆的两个焦点,∠F1PF2=60°,求△F1PF2的面积.
| ||
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点P在椭圆C上,F1,F2是椭圆的两个焦点,∠F1PF2=60°,求△F1PF2的面积.
分析:(I)设椭圆方程为
+
=1(a>b>0),依题意知c=1,当直线l垂直于x轴时,A(c,y0),代入椭圆方程
+
=1可求得a2=2b4,从而可求椭圆C的方程;
(Ⅱ)依题意,利用椭圆的定义与余弦定理可求得|PF1|•|PF2|=
,再利用正弦定理即可求得△F1PF2的面积.
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
(Ⅱ)依题意,利用椭圆的定义与余弦定理可求得|PF1|•|PF2|=
| 4 |
| 3 |
解答: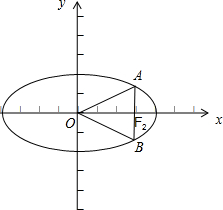 解:(I)设椭圆方程为
解:(I)设椭圆方程为
+
=1(a>b>0),
∵它的一个焦点F2(1,0),即c=1,
∴a2-b2=c2=1①
当直线l垂直于x轴时,A(c,y0),代入椭圆方程
+
=1得:y02=b2(1-
)=
,
∴S△OAB=
|OF2|•|AB|=
×1×2|y0|=
=
,
∴a2=2b4,②
由①②解得a2=2,b2=1,
故椭圆C的方程为
+y2=1.
(Ⅱ)依题意,作图如图: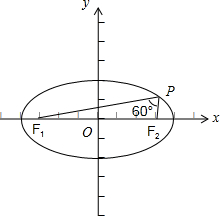
∵|PF1|+|PF2|=2a=2
,|F1F2|=2c=2,∠F1PF2=60°,
∴由余弦定理得:|F1F2|2=|PF1|2+|PF2|2-2|PF1|•|PF2|cos∠F1PF2
=(|PF1|+|PF2|)2-2|PF1|•|PF2|-2|PF1|•|PF2|cos∠F1PF2
=(2
)2-2|PF1|•|PF2|-2|PF1|•|PF2|cos60°
=8-3|PF1|•|PF2|
=4,
∴|PF1|•|PF2|=
,
∴△F1PF2的面积S=
|PF1|•|PF2|sin60°
=
×
×
=
.
 解:(I)设椭圆方程为
解:(I)设椭圆方程为| x2 |
| a2 |
| y2 |
| b2 |
∵它的一个焦点F2(1,0),即c=1,
∴a2-b2=c2=1①
当直线l垂直于x轴时,A(c,y0),代入椭圆方程
| x2 |
| a2 |
| y2 |
| b2 |
| c2 |
| a2 |
| b4 |
| a2 |
∴S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
| b2 |
| a |
| ||
| 2 |
∴a2=2b4,②
由①②解得a2=2,b2=1,
故椭圆C的方程为
| x2 |
| 2 |
(Ⅱ)依题意,作图如图:

∵|PF1|+|PF2|=2a=2
| 2 |
∴由余弦定理得:|F1F2|2=|PF1|2+|PF2|2-2|PF1|•|PF2|cos∠F1PF2
=(|PF1|+|PF2|)2-2|PF1|•|PF2|-2|PF1|•|PF2|cos∠F1PF2
=(2
| 2 |
=8-3|PF1|•|PF2|
=4,
∴|PF1|•|PF2|=
| 4 |
| 3 |
∴△F1PF2的面积S=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 4 |
| 3 |
| ||
| 2 |
=
| ||
| 3 |
点评:本题考查椭圆的性质与椭圆的标准方程,考查椭圆的定义与余弦定理.正弦定理的综合应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
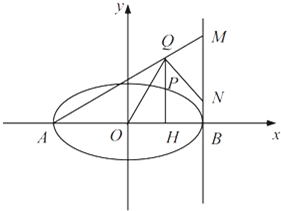 (2013•深圳一模)已知椭圆C 的中心为原点O,焦点在x 轴上,离心率为
(2013•深圳一模)已知椭圆C 的中心为原点O,焦点在x 轴上,离心率为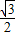 ,且点
,且点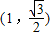 在该椭圆上.
在该椭圆上.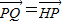 ,直线AQ与过点B 且垂直于x 轴的直线交于点M,
,直线AQ与过点B 且垂直于x 轴的直线交于点M,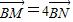 .求证:∠OQN为锐角.
.求证:∠OQN为锐角.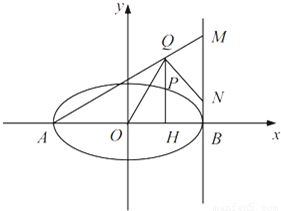
 =
=
 成立,求实数t的值和直线l的方程.
成立,求实数t的值和直线l的方程.