题目内容
已知函数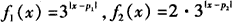 (x∈R,p1,p2为常数),函数f(x)定义为:对每个给定的实数x,
(x∈R,p1,p2为常数),函数f(x)定义为:对每个给定的实数x,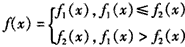 。
。
(1)求f(x)=f1(x)对所有实数x成立的充分必要条件(用p1,p2表示);
(2)设a,b是两个实数,满足a<b且p1,p2∈(a,b),若f(a)=f(b),求证:函数 f(x)在区间[a,b]上的单调增区间的长度之和为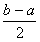 (闭区间[m,n]的长度定义为n-m)。
(闭区间[m,n]的长度定义为n-m)。
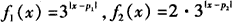 (x∈R,p1,p2为常数),函数f(x)定义为:对每个给定的实数x,
(x∈R,p1,p2为常数),函数f(x)定义为:对每个给定的实数x,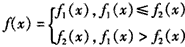 。
。(1)求f(x)=f1(x)对所有实数x成立的充分必要条件(用p1,p2表示);
(2)设a,b是两个实数,满足a<b且p1,p2∈(a,b),若f(a)=f(b),求证:函数 f(x)在区间[a,b]上的单调增区间的长度之和为
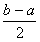 (闭区间[m,n]的长度定义为n-m)。
(闭区间[m,n]的长度定义为n-m)。解:(1)由f(x)的定义可知,f(x)=f1(x)(对所有实数x)等价于f1(x)≤f2(x)(对所有实数x),这又等价于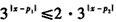 即3|x-p1|-|x -p2|≤2对所有实数x均成立 (*) 易知函数|x-p1|-|x-p2|(x∈R)的最大值为|p2-p1| 故(*)等价于  这就是所求的充分必要条件。 |
|
| (2)分两种情形讨论: (i)当 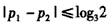 时,由(1)知f(x)=f1(x)(对所有实数x∈[a,b]), 时,由(1)知f(x)=f1(x)(对所有实数x∈[a,b]),则由f(a)=f(b)及a<p1<b易知  再由f1(x) 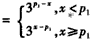 的单调性可知,f(x)在区间[a,b]上的单调增区间的长度为 的单调性可知,f(x)在区间[a,b]上的单调增区间的长度为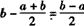 如图所示。 |
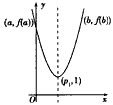 |
(ii)当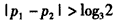 时,不妨设p1<p2则 时,不妨设p1<p2则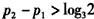 于是,当x≤p1时,有  从而f(x)=f1(x) 当x≥p2时 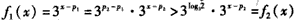 从而 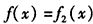 当p1<x<p2时, 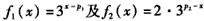 由方程 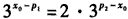 解得f1(x)与f2(x)图象交点的横坐标为  显然 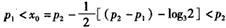 这表明x0在p1与p2之间,由①易知 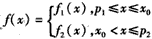 综上可知,在区间[a,b]上 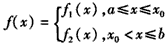 如图所示 故由函数f1(x)与f(x)的单调性可知,f(x)在区间[a,b]上的单调增区间的长度之和为(x0-p1)+(b-p2) 由于f(a)=f(b),即 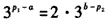 得 得 故由①、②得 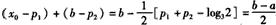 综合(i)、(ii)可知,f(x)在区间[a,b]上的单调增区间的长度之和为 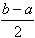 。 。 |
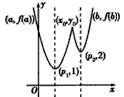 |

练习册系列答案
相关题目
 ,x∈R.
,x∈R. 与
与 的夹角的余弦.
的夹角的余弦. ,x∈R.
,x∈R. 与
与 的夹角的余弦.
的夹角的余弦.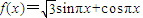 ,x∈R.
,x∈R.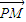 与
与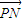 的夹角的余弦.
的夹角的余弦.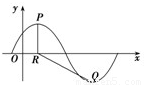 已知函数
已知函数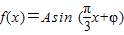 ,x∈R,A>0,
,x∈R,A>0,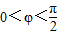 .y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).
.y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).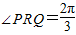 ,求A的值.
,求A的值.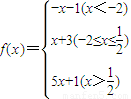 (x∈R),
(x∈R),