题目内容
已知函数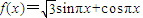 ,x∈R.
,x∈R.(1)求函数f(x)的最大值和最小值;
(2)设函数f(x)在[-1,1]上的图象与x轴的交点从左到右分别为M、N,图象的最高点为P,求
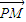 与
与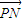 的夹角的余弦.
的夹角的余弦.
【答案】分析:(1)利用两角和差的正弦公式 化简函数的解析式为f(x)= ,根据
,根据 ,
,
求得函数f(x)的最大值和最小值.
(2)令 ,求出M、N两点的坐标,由
,求出M、N两点的坐标,由 ,求出点P的坐标,
,求出点P的坐标,
由 求得结果.
求得结果.
解答: 解:(1)∵
解:(1)∵ =
=
= .
.
∵x∈R,∴ ,
,
∴函数f(x)的最大值和最小值分别为2,-2.
(2)令 ,得
,得 ,
,
∵x∈[-1,1],∴ ,或
,或 ,∴
,∴ ,
,
由 ,且x∈[-1,1]得
,且x∈[-1,1]得  ,∴
,∴ ,
,
∴ ,从而
,从而  =
= .
.
点评:本题考查两角和差的正弦公式,三角函数的最值,两个向量夹角公式的应用,求出M、N两点的坐标,是解题的难点.
 ,根据
,根据 ,
,求得函数f(x)的最大值和最小值.
(2)令
 ,求出M、N两点的坐标,由
,求出M、N两点的坐标,由 ,求出点P的坐标,
,求出点P的坐标,由
 求得结果.
求得结果.解答:
 解:(1)∵
解:(1)∵ =
=
=
 .
.∵x∈R,∴
 ,
,∴函数f(x)的最大值和最小值分别为2,-2.
(2)令
 ,得
,得 ,
,∵x∈[-1,1],∴
 ,或
,或 ,∴
,∴ ,
,由
 ,且x∈[-1,1]得
,且x∈[-1,1]得  ,∴
,∴ ,
,∴
 ,从而
,从而  =
= .
.点评:本题考查两角和差的正弦公式,三角函数的最值,两个向量夹角公式的应用,求出M、N两点的坐标,是解题的难点.

练习册系列答案
相关题目
 (x∈R).若
(x∈R).若 ,
, .求cos2x的值.
.求cos2x的值. ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.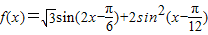 (x∈R).
(x∈R). ,x∈R
,x∈R
 ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.