题目内容
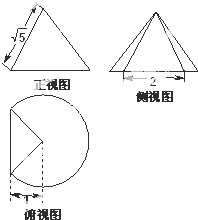 一个圆锥被过顶点的平面截去了较小的一部分几何体,余下的几何体的三视图(如图所示),则余下部分的几何体的表面积为( )
一个圆锥被过顶点的平面截去了较小的一部分几何体,余下的几何体的三视图(如图所示),则余下部分的几何体的表面积为( )分析:由三视图求出圆锥母线,高,底面半径.余下部分的几何体的表面积应为剩余的圆锥侧面,圆锥底面,截面三角形三部分面积之和.
解答:解:由三视图求得,圆锥母线l=
=
,圆锥的高h=
=2,圆锥底面半径为r=
=
截去的底面弧的圆心角为直角,截去的弧长是底面圆周的
,圆锥侧面剩余
,
S1=
πrl=
π×
×
=
底面剩余部分为S2=
πr2+
×
×
=
+1
另外截面三角形面积为S3=
×2×
=
所以余下部分的几何体的表面积为S1+S2+S3=
π+
π+
+1
故选A
(
|
| 6 |
(
|
| l2-h2 |
| 2 |
截去的底面弧的圆心角为直角,截去的弧长是底面圆周的
| 3 |
| 4 |
| 3 |
| 4 |
S1=
| 3 |
| 4 |
| 3 |
| 4 |
| 2 |
| 6 |
3
| ||
| 2 |
底面剩余部分为S2=
| 3 |
| 4 |
| 1 |
| 2 |
| 2 |
| 2 |
| 3π |
| 2 |
另外截面三角形面积为S3=
| 1 |
| 2 |
| 5 |
| 5 |
所以余下部分的几何体的表面积为S1+S2+S3=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 5 |
故选A
点评:本题考查几何体表面积计算.本题关键是弄清几何体的结构特征及表面构成情况,也是易错之处.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 底面是正方形且四个顶点
底面是正方形且四个顶点 在球
在球 的同一个大圆(球面被过球心的平面截得的圆叫做大圆)上,点
的同一个大圆(球面被过球心的平面截得的圆叫做大圆)上,点 在球面上且
在球面上且 面
面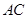 ,且已知
,且已知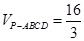 。
。 为
为 中点,求异面直线
中点,求异面直线 与
与 所成角的余弦值。
所成角的余弦值。
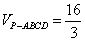
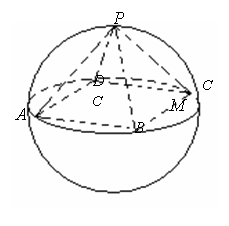 (1)求球
(1)求球